单线性插值
已知中P1点和P2点,坐标分别为(x1, y1)、(x2, y2),要计算 [x1, x2] 区间内某一位置 x 在直线上的y值
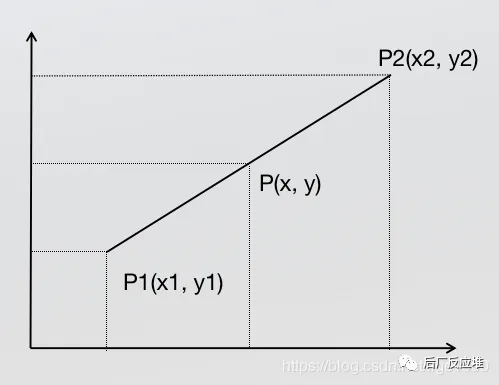
根据初中的知识,2点求一条直线公式(这是双线性插值所需要的唯一的基础公式)
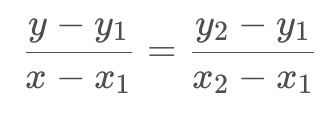
经过简单整理成下面的格式:
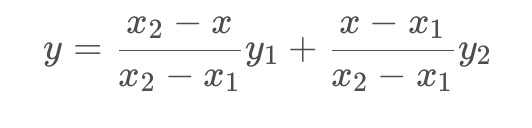
这里没有写成经典的AX+B的形式,因为这种形式从权重的角度更好理解。
首先看分子,分子可以看成x与x1和x2的距离作为权重,这也是很好理解的,P点与P1、P2点符合线性变化关系,所以P离P1近就更接近P1,反之则更接近P2。
现在再把公式中的分式看成一个整体,原式可以理解成y1与y2是加权系数,如何理解这个加权,要返回来思考一下,咱们先要明确一下根本的目的:咱们现在不是在求一个公式,而是在图像中根据2个点的像素值求未知点的像素值。这样一个公式是不满足咱们写代码的要求的。 现在根据实际的目的理解,就很好理解这个加权了,y1与y2分别代表原图像中的像素值,上面的公式可以写成如下形式:
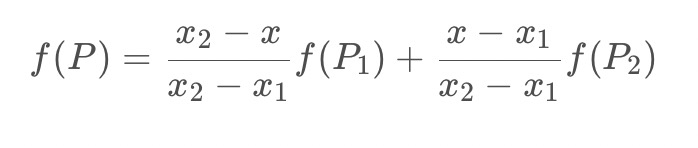
双线性插值
已知Q11(x1,y1)、Q12(x1,y2)、Q21(x2,y1)、Q22(x2,y2),求其中点P(x,y)的值。
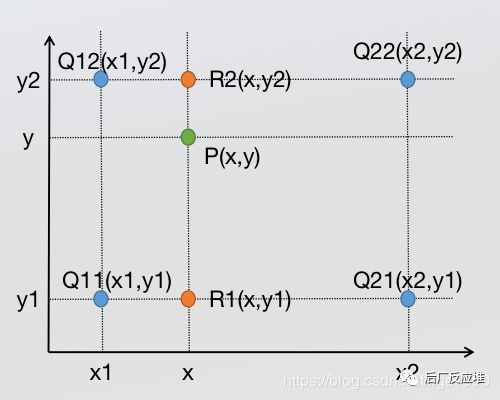
前面介绍过双线性插值是分别在两个方向计算了共3次单线性插值,如图所示,先在x方向求2次单线性插值,获得R1(x, y1)、R2(x, y2)两个临时点,再在y方向计算1次单线性插值得出P(x, y)(实际上调换2次轴的方向先y后x也是一样的结果)。 1.x方向单线性插值 直接带入前一步单线性插值最后的公式
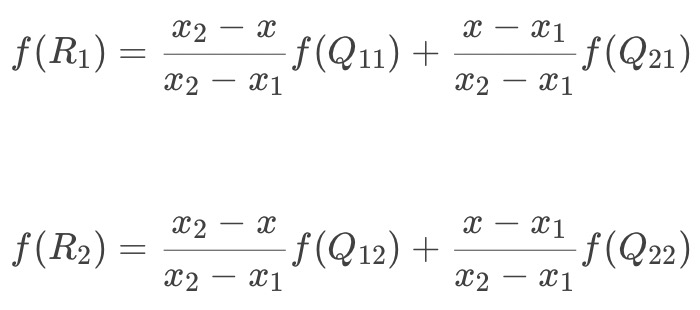
2.y方向单线性插值
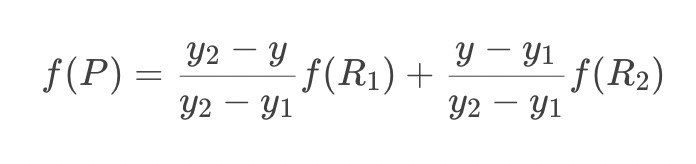
将第一步结果带入第二步
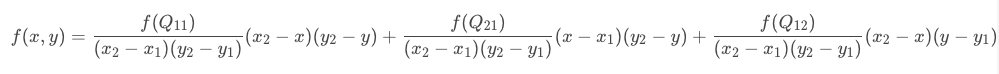
回顾一下上面双线性插值对应关系的图,不难发现,在计算中有这样的关系:
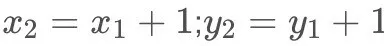
那么上面的公式中的分母全都为1,如下:
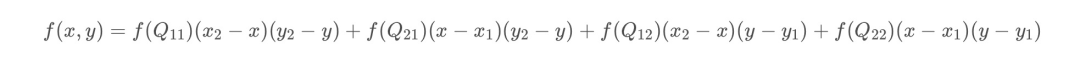
在有些资料中,会写成权重的形式,上面的展开式是下面的权重表达式的正确求法
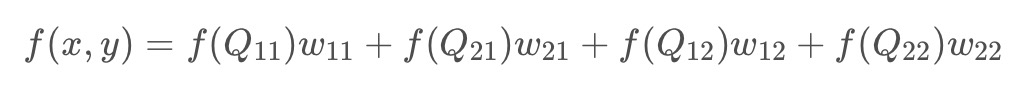

此处评论已关闭