原理解释1
Dijkstra算法是一种经典的图搜索算法,用于求解带权重图中的最短路径问题。它的原理如下:
-
初始化:将起始节点的距离设为0,将所有其他节点的距离设为无穷大(或一个较大的值)。将所有节点标记为未访问状态。
-
选择当前节点:从未访问的节点中选择一个距离最小的节点作为当前节点。
-
更新邻居节点的距离:对于当前节点的每个邻居节点,计算通过当前节点到达邻居节点的距离。如果这个距离小于邻居节点当前的距离,则更新邻居节点的距离。
-
标记当前节点为已访问:将当前节点标记为已访问。
-
重复步骤2-4,直到所有节点都被标记为已访问,或者目标节点被访问。
-
构建最短路径:从目标节点开始,通过每个节点的最短路径父节点指针,逆向构建最短路径。
Dijkstra算法通过不断更新节点的距离值,从起始节点开始逐步扩展搜索,直到找到目标节点或者遍历了所有可达节点。它保证在每一次选择当前节点时,当前节点的距离是已知的最小值,因此在遇到目标节点时,得到的路径就是最短路径。
需要注意的是,Dijkstra算法适用于无负权重边的图。如果图中存在负权重边,可以考虑使用其他算法,如Bellman-Ford算法或A*算法。
总结起来,Dijkstra算法是一种用于求解带权重图中最短路径的经典算法。它通过不断更新节点的距离值,选择当前最短路径的节点,直到找到目标节点或遍历完所有可达节点。
原理解释2
Dijkstra算法是一种用于求解图中单源最短路径的经典算法。它可以找到从给定起始节点到图中所有其他节点的最短路径。
以下是Dijkstra算法的原理步骤:
-
创建一个空的距离表(distance table)和一个空的前驱表(predecessor table)来存储节点的最短路径信息。
-
将起始节点标记为当前节点,并将其距离设置为0。将其他节点的距离设置为无穷大(或一个较大的值)。
-
选择当前节点,并计算从起始节点到当前节点经过的路径长度。
-
遍历当前节点的所有邻居节点(即与当前节点相连的节点),并更新它们的距离。如果通过当前节点到达邻居节点的路径比之前计算的路径更短,则更新邻居节点的距离,并将当前节点设置为邻居节点的前驱节点。
-
标记当前节点为已访问。
-
从尚未访问的节点中选择下一个最短路径节点作为当前节点,即选择距离表中具有最小距离的节点。
-
重复步骤4至步骤6,直到所有节点都被访问或无法到达的节点已被标记。
-
最终,距离表中存储了从起始节点到每个节点的最短路径长度,前驱表中存储了每个节点的前驱节点信息,可以根据前驱表反向追溯最短路径。
Dijkstra算法的关键思想是通过每次选择距离起始节点最近的节点,逐步扩展最短路径的范围,直到到达目标节点或访问完所有节点。该算法保证了在有向无环图(DAG)中的正确性,但不适用于存在负权边的图。
Dijkstra算法的时间复杂度取决于图的规模,通常为$O(|V|^2)$,其中|V|是节点的数量。为了提高效率,可以使用优先队列(如最小堆)来选择下一个最短路径节点,将时间复杂度优化为O((|V| + |E|) log |V|),其中|E|是边的数量。
Dijkstra算法图文详解
Dijkstra算法
Dijkstra算法算是贪心思想实现的,首先把起点到所有点的距离存下来找个最短的,然后松弛一次再找出最短的,所谓的松弛操作就是,遍历一遍看通过刚刚找到的距离最短的点作为中转站会不会更近,如果更近了就更新距离,这样把所有的点找遍之后就存下了起点到其他所有点的最短距离。
问题引入:
指定一个点(源点)到其余各个顶点的最短路径,也叫做“单源最短路径”。例如求下图中的1号顶点到2、3、4、5、6号顶点的最短路径。
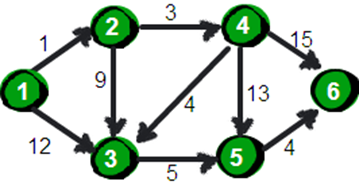
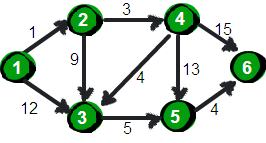


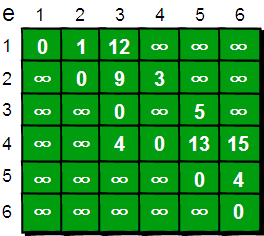



下面我们来模拟一下:
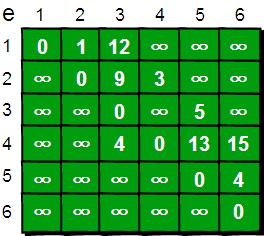
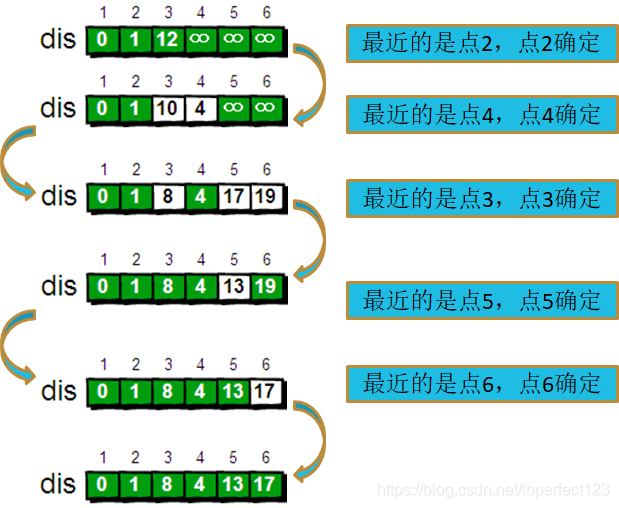
这就是Dijkstra算法的基本思路。
Dijkstra算法详解 通俗易懂 - 知乎 (zhihu.com)
[Dijkstra算法图文详解_black-hole6的博客-CSDN博客](
