测试环境
由于这是一个Python语言的软件包,因此需要你的机器上首先安装好Python语言的环境。关于这一点,请自行在网络上搜索获取方法。
关于如何安装Matplotlib请参见这里:Matplotlib Installing。
本文中的源码和测试数据可以在这里获取:Github: matplotlib_tutorial
本文的代码示例会用到其他一些Python库。建议读者先对其有一定的熟悉,我的博客中也有一些相关文章。
本文的代码在如下环境中测试:
- Apple OS X 10.13
- Python 3.6.2
- matplotlib 2.2.3
- numpy 1.14.1
准备
绘制3D图形的时候我们通常都会包含下面这个代码片段,这里我们先对其进行说明。
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure()
ax = fig.gca(projection='3d')
这4行代码说明如下:
- 第一行自然不必说,就是导入
matplotlib.pyplot。 - 第二行
from mpl_toolkits.mplot3d import Axes3D是导入Axes3D类。我们后面在绘制3D图形的时候,相应的函数都位于这个接口上。 -
fig = plt.figure()是获取到当前figure对象。 -
ax = fig.gca(projection='3d')这一行是比较关键的。fig.gca是获取图中的当前极轴。如果不存在,或者不是极轴,则将创建相应的轴,然后返回。此时得到的ax对象的类型是Axes3D的子类,这个对象将是绘制3D图形的入口。
Colormap
绘制图形的时候,常常会需要对图形着色。Matplotlib中内置了很多的Colormap来简化这个工作,具体可以看这里:Choosing Colormaps。
下面是一些Colormap示例:
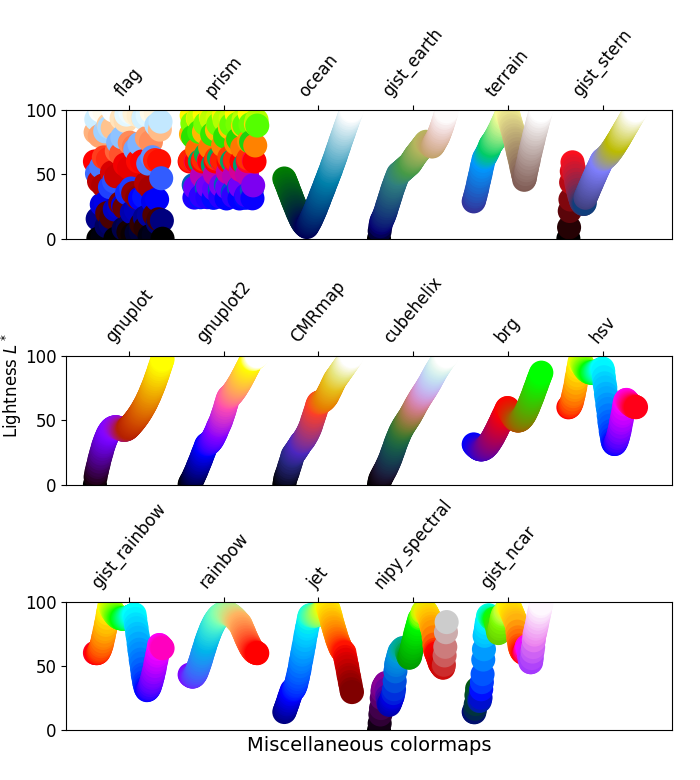
通过指定相应的名称我们就可以直接使用这里的Colormap了。
线形图
Axes3D.plot 函数用来绘制线形图。
首先我们来看最简单的图形 - 线形图。
由于这是三维空间中的线,所以需要若干个(x, y, z)坐标的值。
下面这段代码生成了一条三维空间中的直线。
# line.py
import matplotlib.pyplot as plt
import numpy as np
from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure()
ax = fig.gca(projection='3d')
x = np.linspace(-10, 10, 1000)
y = np.linspace(-10, 10, 1000)
z = np.add(x, y)
ax.plot(x, y, z)
plt.show()
从这段代码可以看出,这条线的x和y轴的范围都是[-10, 10]。我们共计采样了1000个点。
需要注意的是,由于线是通过点来描绘的,每一个点都由[x,y,z]三个坐标值来确定,因此这里x,y,z三个数组的元素数量应该是一样多的。
z轴取值为np.add(x, y)。请注意,np.add是元素级(element-wise)的运算:它是将x和y两个数组的元素逐个相加,所以得到的结果仍然是包含了1000个元素的数组。
这段代码得到的结果如下:
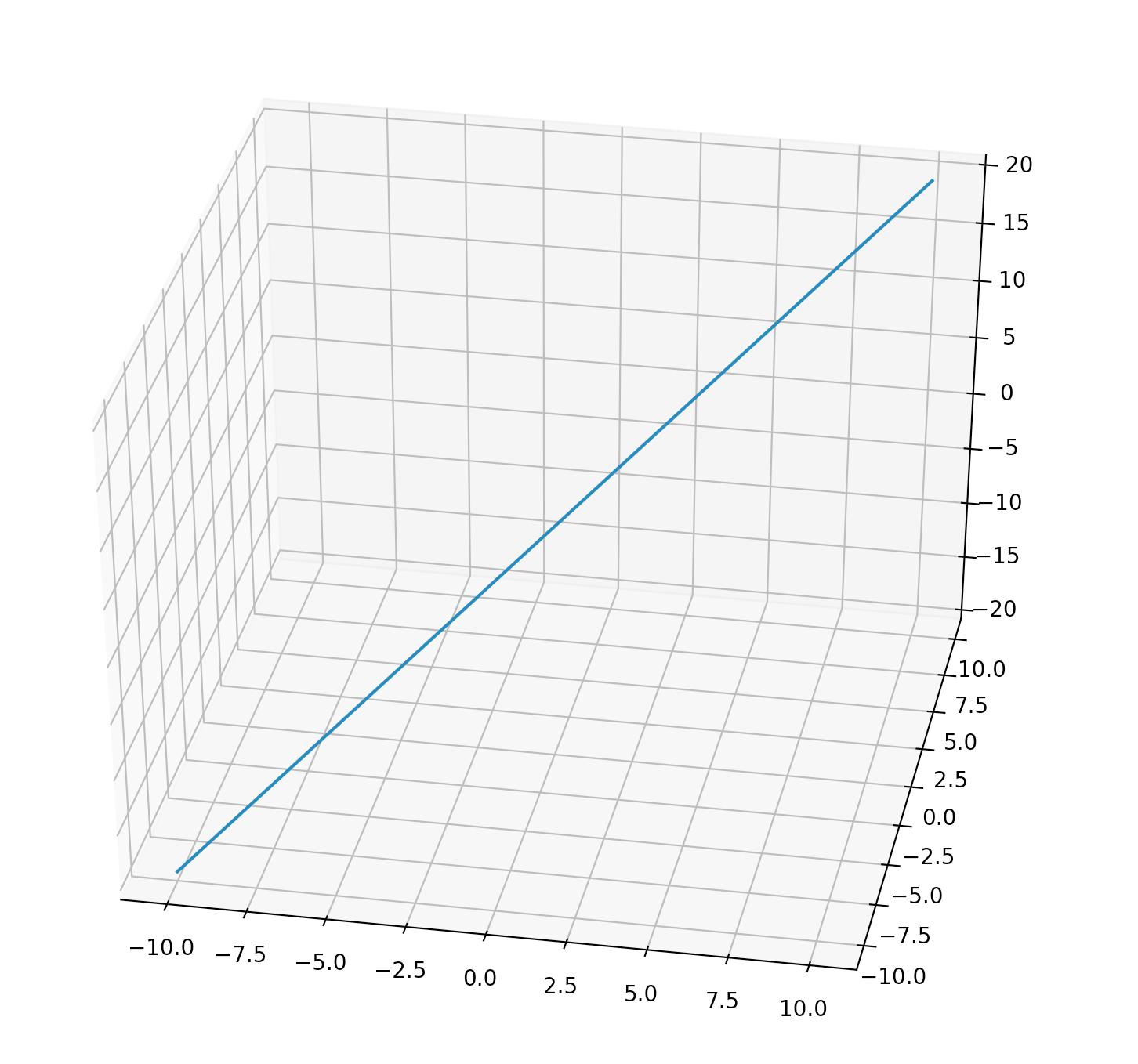
散点图
Axes3D.scatter 函数用来绘制散点图。
下面我们再来看一下散点图。
和线形图类似,它也是展示若干个(x, y, z)坐标的值。区别在于,这里仅仅是一些点,没有通过线连在一起。
下面是一段代码示例:
# scatter.py
import matplotlib.pyplot as plt
import numpy as np
from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure()
ax = fig.gca(projection='3d')
count = 100
range = 100
xs = np.random.rand(count) * range
ys = np.random.rand(count) * range
zs = np.random.rand(count) * range
ax.scatter(xs, ys, zs, s=zs, c=zs)
ax.set_xlabel('X Label')
ax.set_ylabel('Y Label')
ax.set_zlabel('Z Label')
plt.show()
这段代码中,我们还设置了三个坐标轴的Label。
另外,所有点的x,y,z轴都是随机的。范围都在100以内。并且,我们在显示这些点的时候,根据z值的大小设置了点的颜色和尺寸以示区分。
最终我们得到的图形如下所示:
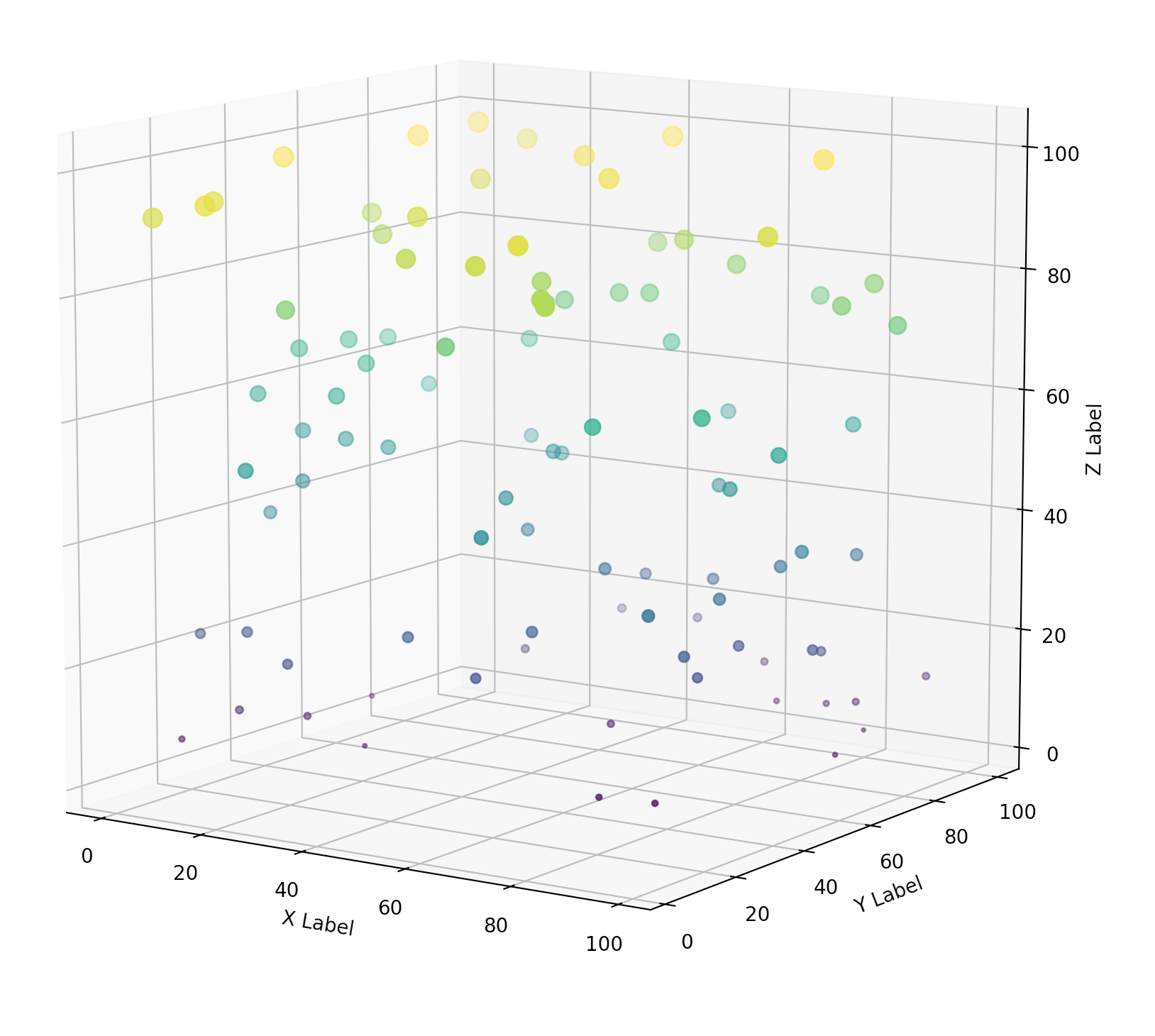
线框图
Axes3D.plot_wireframe 函数用来绘制线框图。
线框图要比前面的图形要复杂一些。
线框图展示的是一个曲面的框架结构,由于是一个面,因此它在x,y两个坐标的整个面上都应该有所取值。
前面两种图形的x,y轴的值都是一维的数组,而对于线框图来说,其x,y轴的取值应该是一个二维的矩阵。
例如,我们设置x的范围是[1, 3]之间,y的范围是[11, 15]之间。并且,每一个整数坐标取一个点,那么如下的所有点上都会对应一个z值:
([1,11],[2,11],[3,11] [1,12],[2,12],[3,12] [1,13],[2,13],[3,13] [1,14],[2,14],[3,14] [1,15],[2,15],[3,15])\begin{pmatrix} [1,11], [2,11], [3,11] \\ [1,12], [2,12], [3,12] \\ [1,13], [2,13], [3,13] \\ [1,14], [2,14], [3,14] \\ [1,15], [2,15], [3,15] \end{pmatrix} ⎝⎛[1,11],[2,11],[3,11] [1,12],[2,12],[3,12] [1,13],[2,13],[3,13] [1,14],[2,14],[3,14] [1,15],[2,15],[3,15]⎠⎞
而对于描述x,y轴的两个数组来说,它们各自应该是下面这样的矩阵:
(1,2,3 1,2,3 1,2,3 1,2,3 1,2,3)\begin{pmatrix} 1, 2, 3 \\ 1, 2, 3 \\ 1, 2, 3 \\ 1, 2, 3 \\ 1, 2, 3 \end{pmatrix} ⎝⎛1,2,3 1,2,3 1,2,3 1,2,3 1,2,3⎠⎞
(3)
(11,11,11 12,12,12 13,13,13 14,14,14 15,15,15)\begin{pmatrix} 11, 11, 11 \\ 12, 12, 12 \\ 13, 13, 13 \\ 14, 14, 14 \\ 15, 15, 15 \end{pmatrix} ⎝⎛11,11,11 12,12,12 13,13,13 14,14,14 15,15,15⎠⎞
这里的两个矩阵其实是互相由对方数据的数量而确定尺寸的。
numpy中的meshgrid函数刚好可以帮我们完成这个功能,下面是一段代码示例:
# meshgrid_demo.py
import numpy as np
x = np.arange(1, 4)
y = np.arange(11, 16)
print(x)
print(y)
X, Y = np.meshgrid(x, y)
print(X)
print(Y)
请仔细观察一下它的输出:
[1 2 3]
[11 12 13 14 15]
[[1 2 3]
[1 2 3]
[1 2 3]
[1 2 3]
[1 2 3]]
[[11 11 11]
[12 12 12]
[13 13 13]
[14 14 14]
[15 15 15]]
有了这个基础之后,我们就可以以此来产生我们需要的线框图了。
假设我们要展示的函数如下:
z=−x3+y4,−10<x,y<10z = -x^3 + y^4 , -10 \lt x,y \lt 10 z=−x3+y4,−10<x,y<10
我们可以通过下面这段代码来生成这个函数的图形:
# wireframe.py
import matplotlib.pyplot as plt
import numpy as np
from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure()
ax = fig.gca(projection='3d')
x = np.arange(-10, 10, 0.1)
y = np.arange(-10, 10, 0.1)
X, Y = np.meshgrid(x, y)
Z = np.add(-np.power(X, 3), np.power(Y, 4))
surf = ax.plot_wireframe(X, Y, Z)
plt.show()
请注意,这段代码中关于
np的函数都是元素级(element-wise)的运算。请读者思考一下,
np.power(X, 3)与X**3的含义分别是什么。
这段代码所得到的图形如下所示:
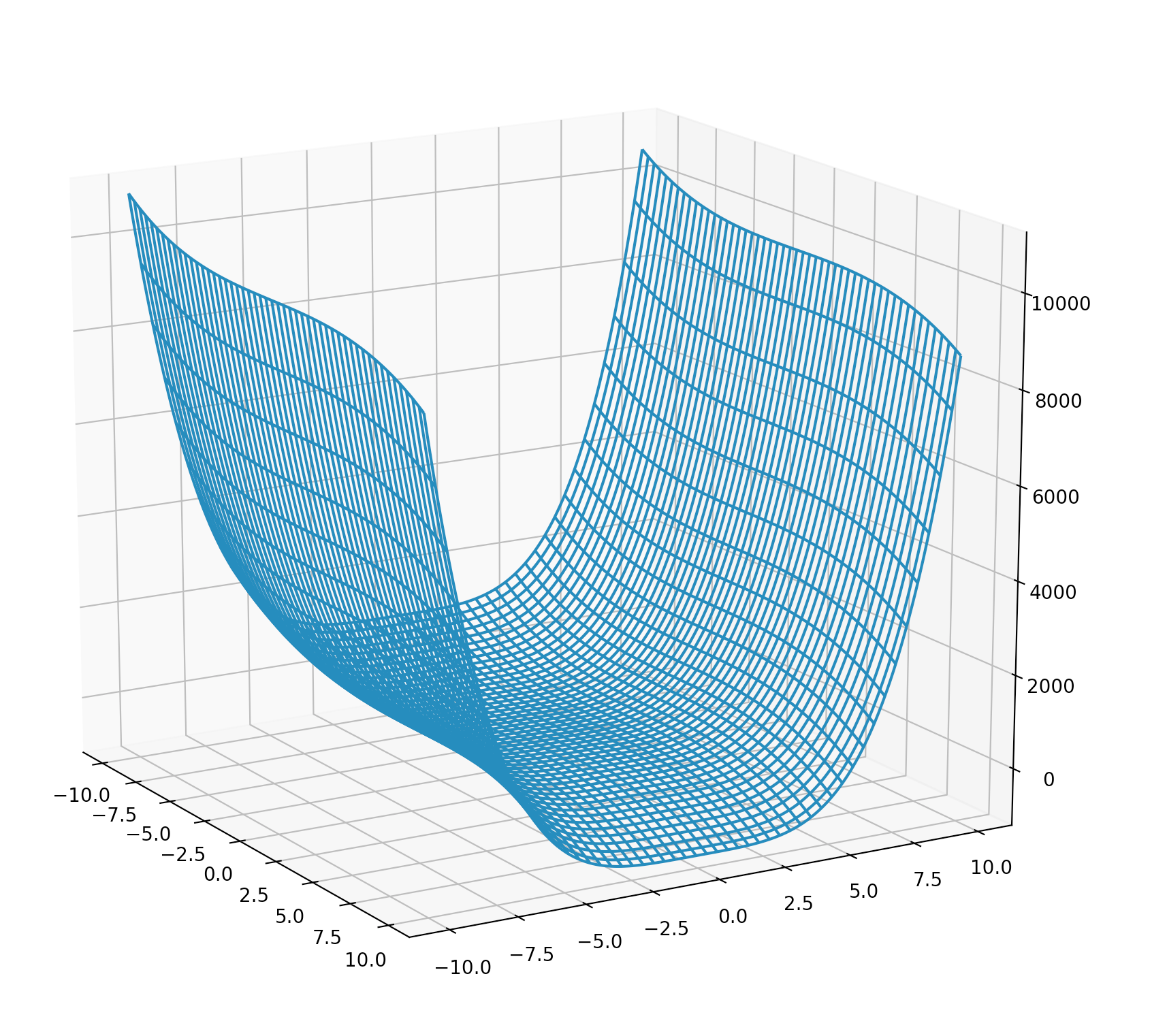
曲面图
Axes3D.plot_surface 函数用来绘制曲面图。
曲面图和线框图类似,它们都是描述三维空间中的曲面的。区别在于:曲面图中的面是着色的。
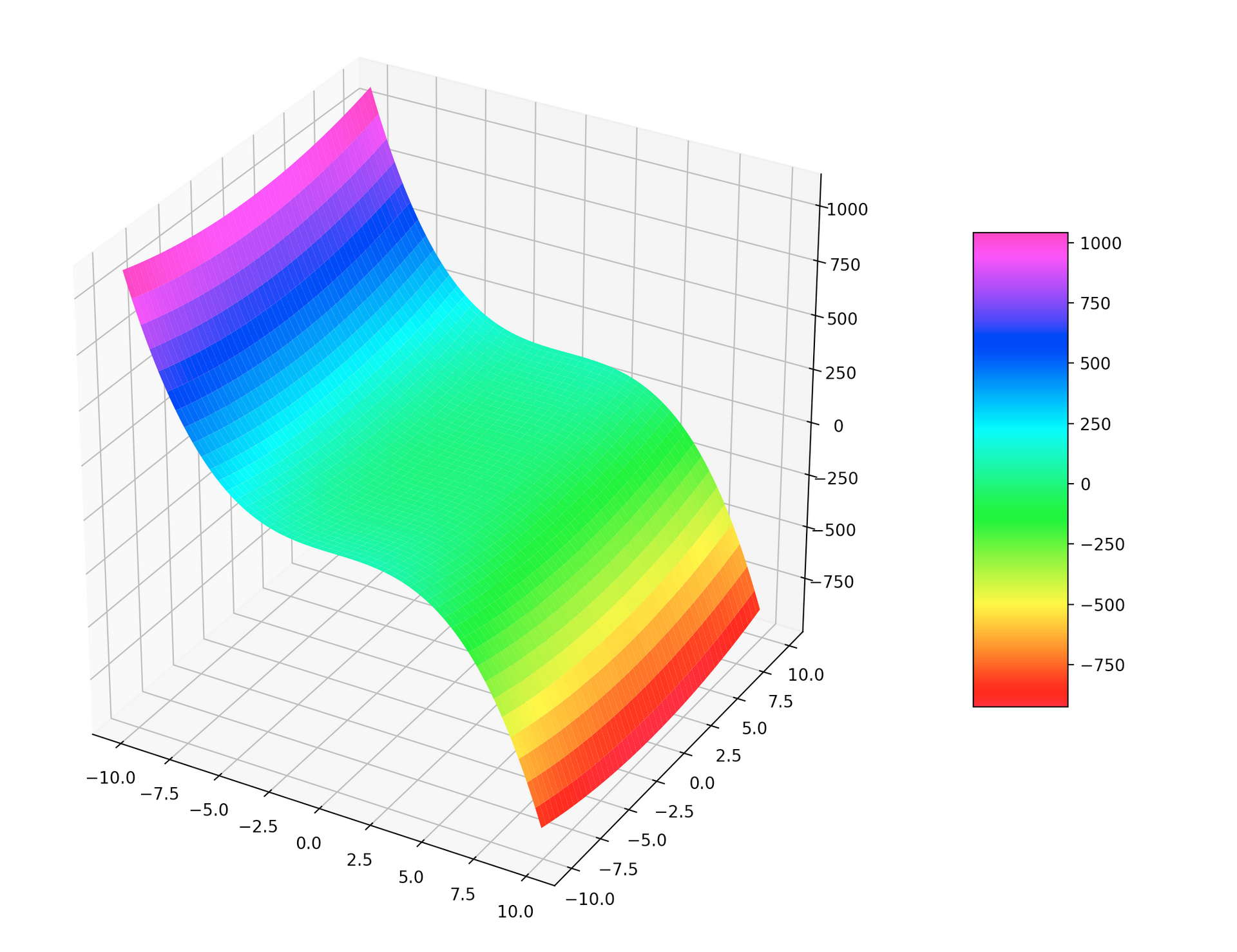
下面这段代码绘制出了下面这个函数的图形:
z=−x3+y2,−10<x,y<10z = -x^3 + y^2, -10 \lt x, y \lt 10 z=−x3+y2,−10<x,y<10
# surface.py
import matplotlib.pyplot as plt
import numpy as np
from matplotlib import cm
from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure()
ax = fig.gca(projection='3d')
x = np.arange(-10, 10, 0.1)
y = np.arange(-10, 10, 0.1)
X, Y = np.meshgrid(x, y)
Z = np.add(-np.power(X, 3), np.power(Y, 2))
surf = ax.plot_surface(X, Y, Z, cmap=cm.gist_rainbow)
fig.colorbar(surf, shrink=0.5, aspect=5)
plt.show()
这段代码整体应该都不难理解,只有两个地方需要说明一下:
- 这里通过
cmap=cm.gist_rainbow指定了曲面的颜色。更多的Colormap请到查阅这里:Choosing Colormaps。 - 通过
fig.colorbar(surf, shrink=0.5, aspect=5)添加了一个色彩条。shrink指定了色彩条与图形高度的比例,aspect指定了色彩条本身的长宽比。
这段代码得到的图形如下所示:
等高线
Axes3D.contour 函数用来绘制等高线。
等高线顾名思义,就是描述高度相等的线。等高线通常伴随主体图形一起出现,辅助我们观察主体图形的一些特性。
有了前面的基础,绘制等高线也就很容易了。
下面这段代码绘制出了以下这个函数的线框图以及等高线:
Z=−x4+Y4,−10<x,y<10Z = -x^4 + Y^4, -10 \lt x, y \lt 10 Z=−x4+Y4,−10<x,y<10
# contour.py
import matplotlib.pyplot as plt
import numpy as np
from matplotlib import cm
from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure()
ax = fig.gca(projection='3d')
x = np.arange(-10, 10, 0.1)
y = np.arange(-10, 10, 0.1)
X, Y = np.meshgrid(x, y)
Z = np.add(-np.power(X, 4), np.power(Y, 4))
ax.set_xlabel("X")
ax.set_ylabel("Y")
ax.plot_wireframe(X, Y, Z, alpha=0.1)
ax.contour(X, Y, Z, cmap=cm.Accent, linewidths=2)
plt.show()
为了便于观察等高线,我们将主体图形的线框图透明度设为0.1,然后将等高线的粗度设置为2。
上面这段代码得到的图形如下所示:
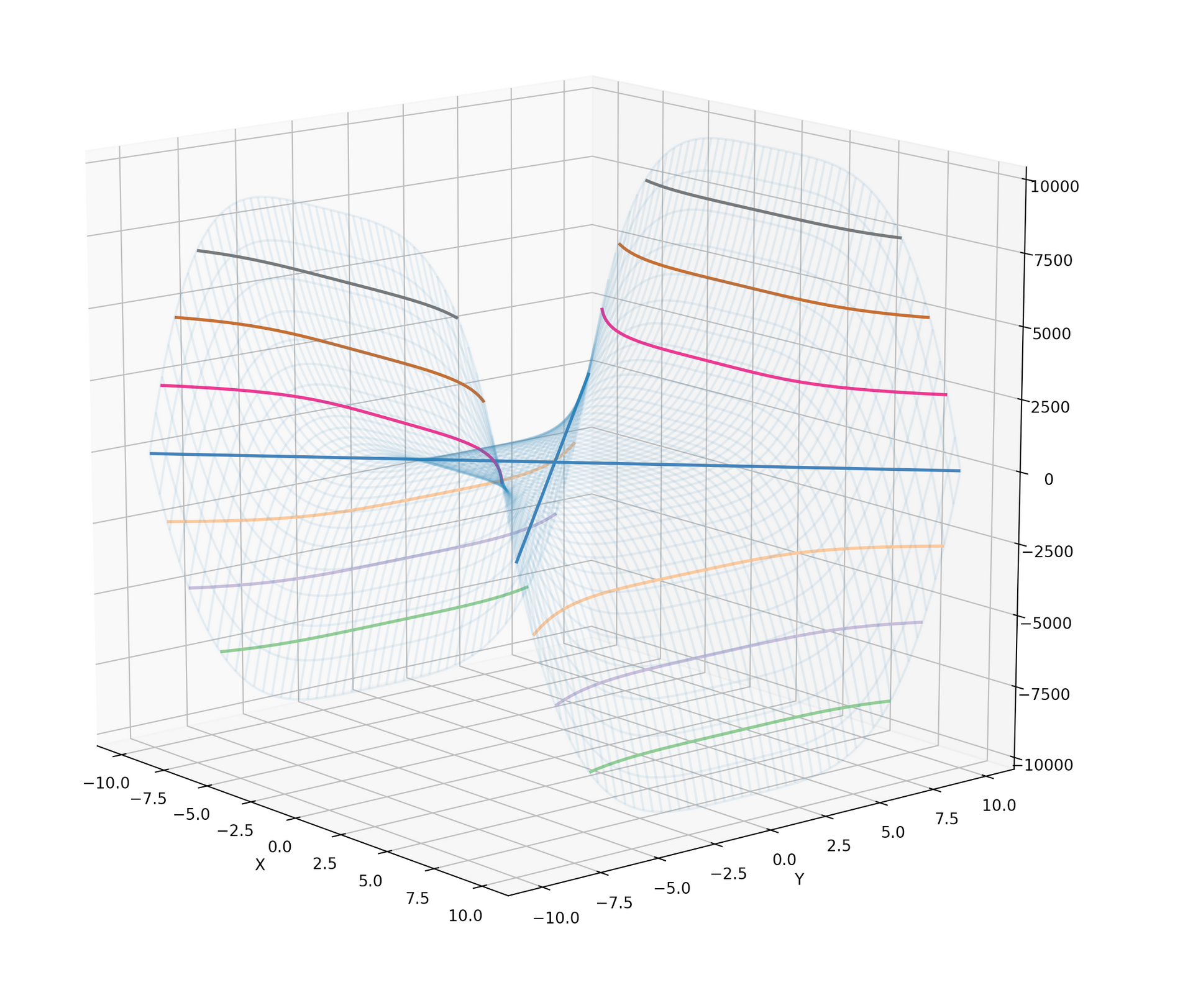
这个图形比较复杂,单从一个角度不太容易看清楚其完整结构,文末我们会讲解怎么制作一副动态图来展示图形的全貌。
柱状图
Axes3D.bar 函数用来绘制柱状图。
柱状图也是很常用的图。
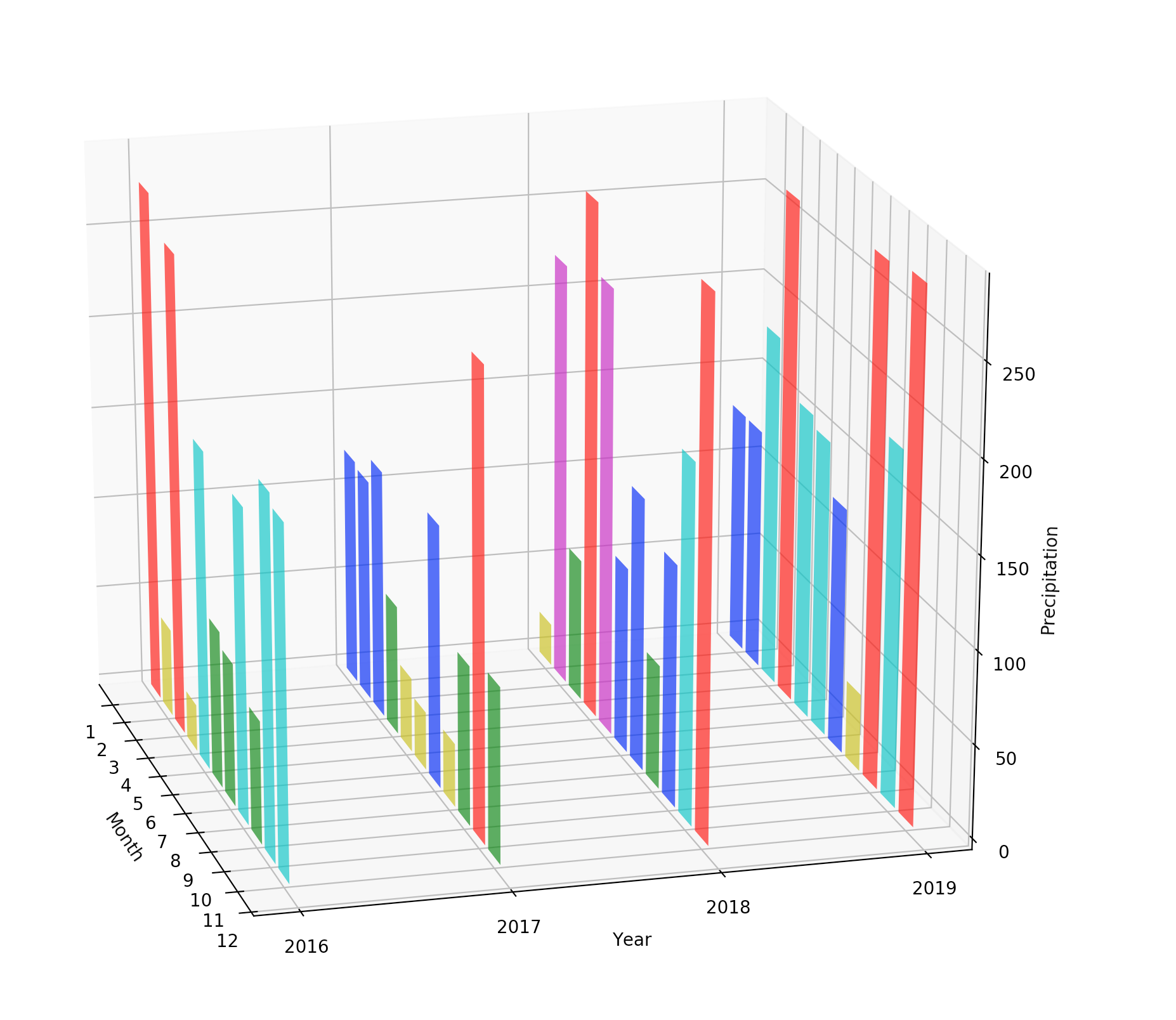
下面这段代码展示了这样一种场景:在一副图中,对比一个城市四年期间每个月的降水量。
在这幅图中,每一年的12个月是一组柱状图。四年的数据进行了前后的对比展示。
代码如下:
# bar.py
import matplotlib.pyplot as plt
import numpy as np
from matplotlib.collections import PolyCollection
from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure()
ax = fig.gca(projection='3d')
np.random.seed(59)
month = np.arange(1, 12)
years = [2016, 2017, 2018, 2019]
def get_color(value_array):
color = []
for v in value_array:
if (v < 50):
color.append('y')
elif (v < 100):
color.append('g')
elif (v < 150):
color.append('b')
elif (v < 200):
color.append('c')
elif (v < 250):
color.append('m')
else:
color.append('r')
return color
for year, c in zip(years, ['b','c','r','m']):
value = np.random.rand(len(month)) * 300
ax.bar(month, value, year, zdir='y', color=get_color(value), alpha=0.7)
for i in np.arange(0, 12):
ax.bar
ax.set_xlabel('Month')
ax.set_xticks(np.arange(1, 13))
ax.set_ylabel('Year')
ax.set_yticks(np.arange(2016, 2020))
ax.set_zlabel('Precipitation')
plt.show()
在这段代码中,我们通过随机数生成了每个月的降水量。并且根据降水量的程度设置了条柱的颜色以示区分。
我们最终得到的图形如下所示:
多边形
Axes3D.add_collection3d 函数用来向图形中添加3D集合对象。
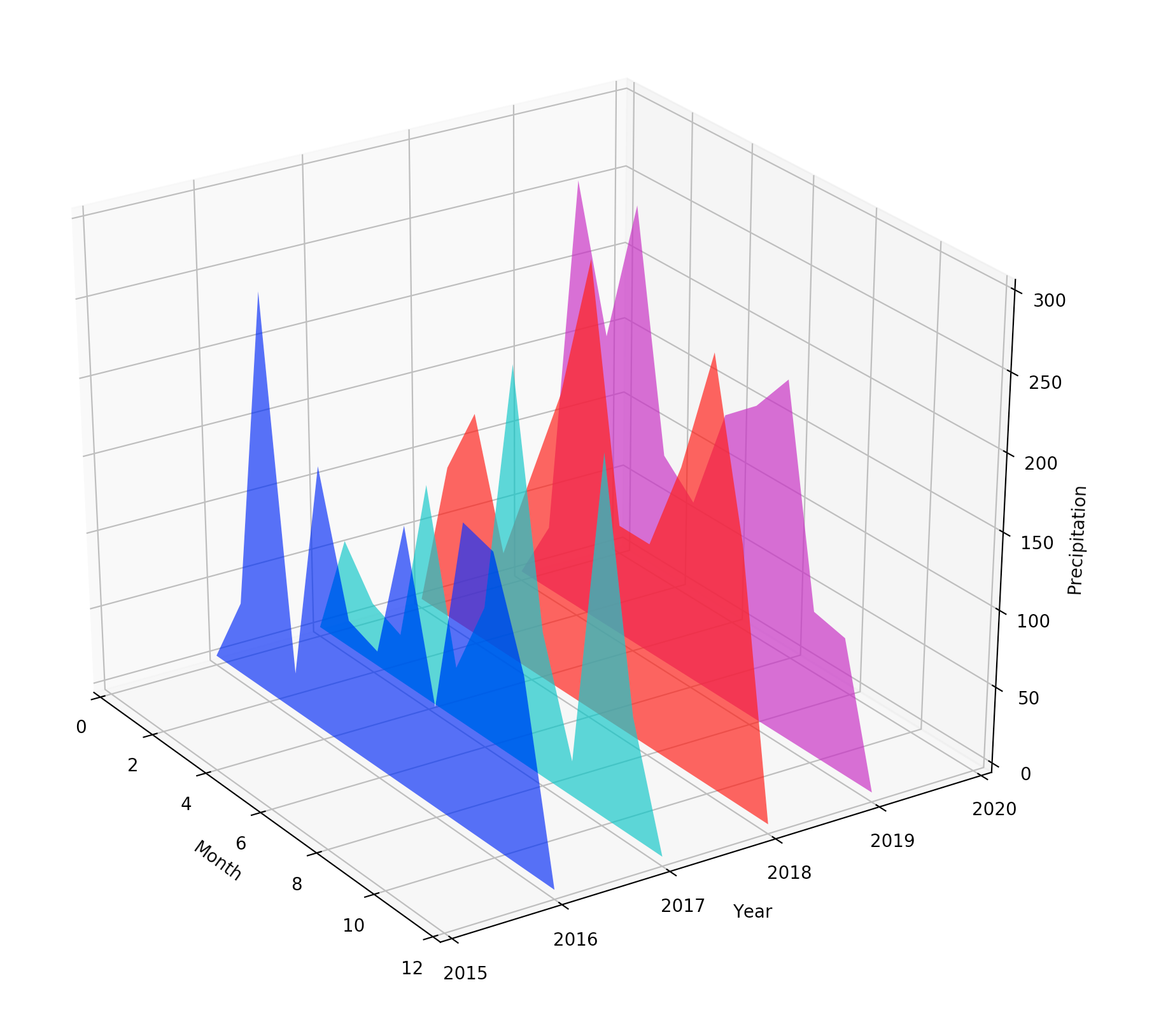
对于某些数据(例如降水量)来说,我们也可能希望通过多边形来了解其每个点的走势。
下面这段代码通过多边形的形式展示了和上面柱状图一样的数据。
# poly.py
import matplotlib.pyplot as plt
import numpy as np
from matplotlib.collections import PolyCollection
from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure()
ax = fig.gca(projection='3d')
np.random.seed(59)
month = np.arange(0, 13)
years = [2016, 2017, 2018, 2019]
precipitation = []
for year in years:
value = np.random.rand(len(month)) * 300
value[0], value[-1] = 0, 0
precipitation.append(list(zip(month, value)))
poly = PolyCollection(precipitation, facecolors=['b','c','r','m'])
poly.set_alpha(0.7)
ax.add_collection3d(poly, zs=years, zdir='y')
ax.set_xlabel('Month')
ax.set_xlim3d(0, 12)
ax.set_ylabel('Year')
ax.set_ylim3d(2015, 2020)
ax.set_zlabel('Precipitation')
ax.set_zlim3d(0, 300)
plt.show()
Axes3D.add_collection3d 函数除了支持PolyCollection,还支持LineCollection和PatchCollection。这一点,读者可以自行研究一下。
上面这段代码得到的图形如下:
制作动图
很多时候,我们可能需要制作一张动画图来展示图形的全貌,下面我们就来看一下如何做到。
生成不同角度的图形
为了制作动图,我们需要先有制作动图的图片素材。
下面我们就以前面等高线那个函数生成的复杂图形为例,来看看如何生成一个关于这个图形不同角度的动图。
相关代码如下:
# surface_files.py
import matplotlib.pyplot as plt
import numpy as np
from matplotlib import cm
from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure(figsize=(10, 8))
ax = fig.gca(projection='3d')
x = np.arange(-10, 10, 0.1)
y = np.arange(-10, 10, 0.1)
X, Y = np.meshgrid(x, y)
Z = np.add(-np.power(X, 4), np.power(Y, 4))
ax.set_xlabel("X")
ax.set_ylabel("Y")
ax.plot_surface(X, Y, Z, cmap=cm.hsv)
for angle in range(95, 180, 3):
ax.set_zlabel("Angle: " + str(angle))
ax.view_init(30, angle)
filename = "./" + str(angle) + ".png"
plt.savefig(filename)
print("Save " + filename + " finish")
这段代码其实并不复杂,与前面的区别主要就是在于代码最后的for循环。
在这个for循环中,我们选取了从95到180这个范围的角度,每隔3做一次采样,每次采样做如下的事情:
- 通过
set_zlabel设置了当前旋转角度的Label - 通过
ax.view_init(30, angle)设置图形的视角 - 根据当前角度生成一个单独的文件名称
- 通过
plt.savefig(filename)保存文件 - 打印日志
这段代码执行完成之后,我们就会得到一系列的png文件。下面我们就通过这些png文件来生成动图。
使用ImageMagick
这里通过一个免费的跨平台工具ImageMagick来制作动图。该工具支持 Linux,Windows,Mac OS X,iOS和Android等各个平台。
首先,我们到这里进行下载:Download ImageMagick。
请根据你的平台选择下载哪个版本。
由于我是Mac用户,所以直接通过下面的命令就可以安装ImageMagick。
brew install ImageMagick
安装好之后,命令行就会有convert工具。通过这个工具就可以生成动图了。
相关命令如下:
convert -delay 50 *.png animated.gif
当然,你可以研究一下这个命令的其他参数和功能。这里就不赘述了。
我们最终得到的动图看起来像下面这个样子:
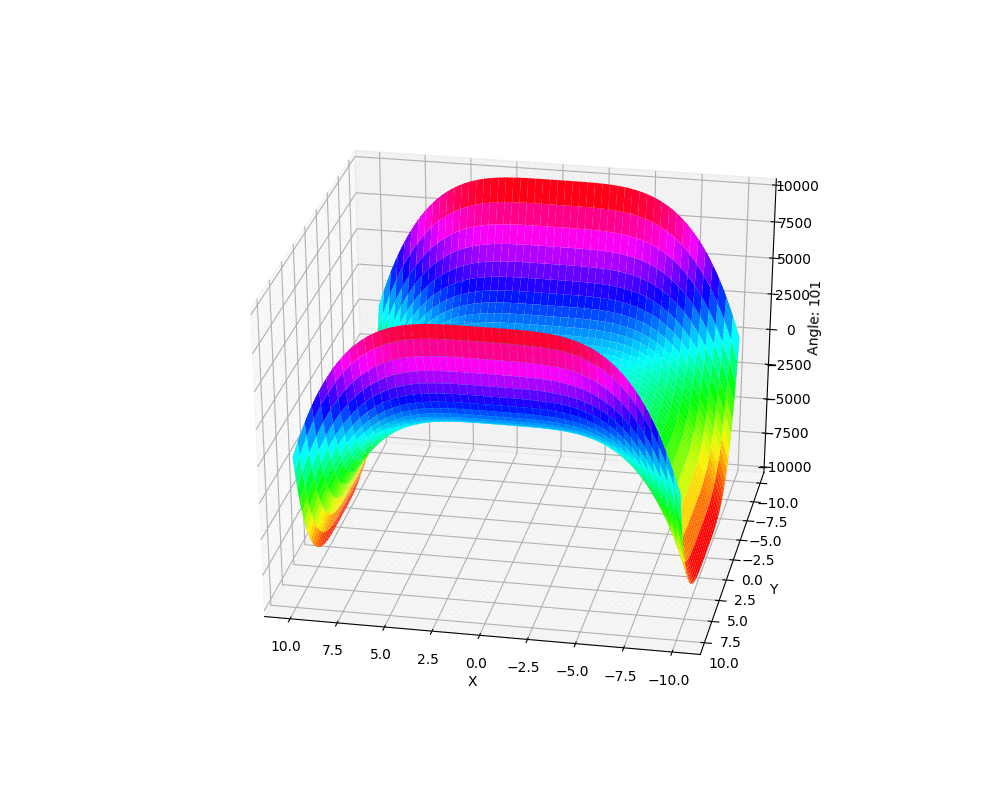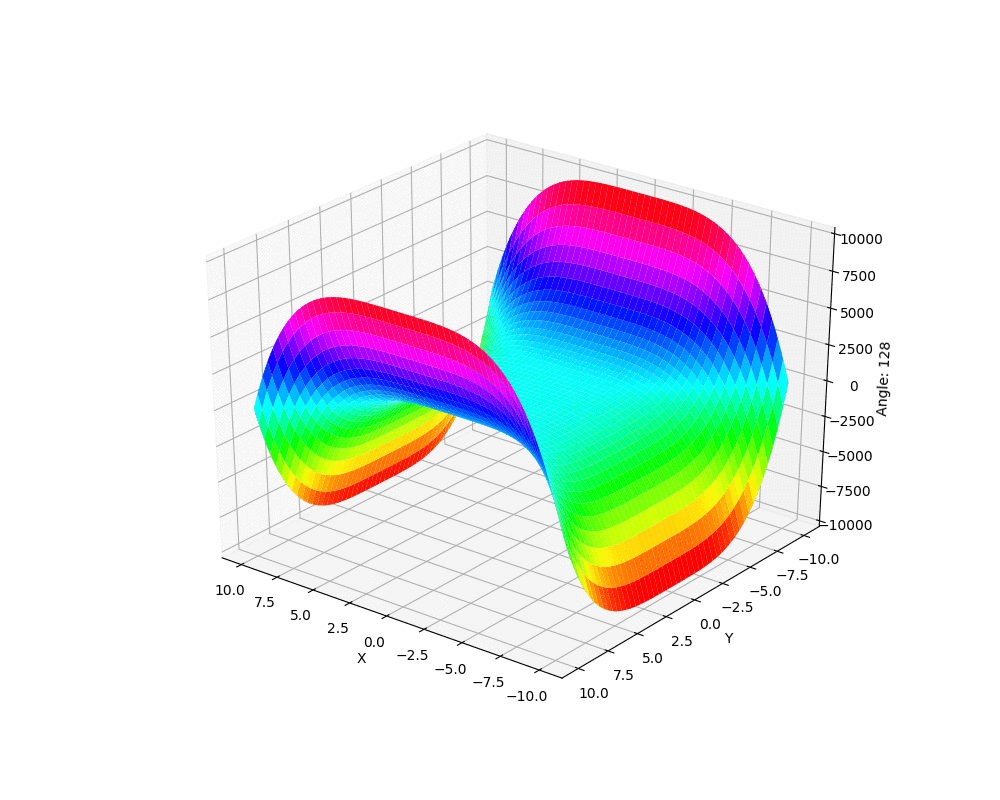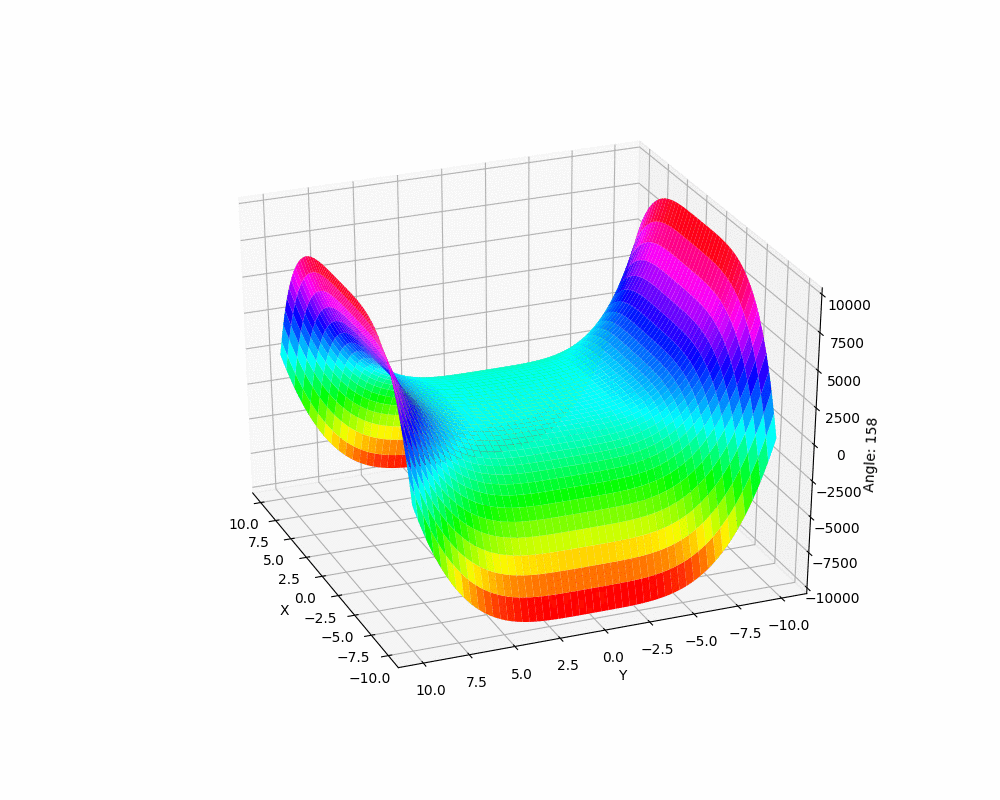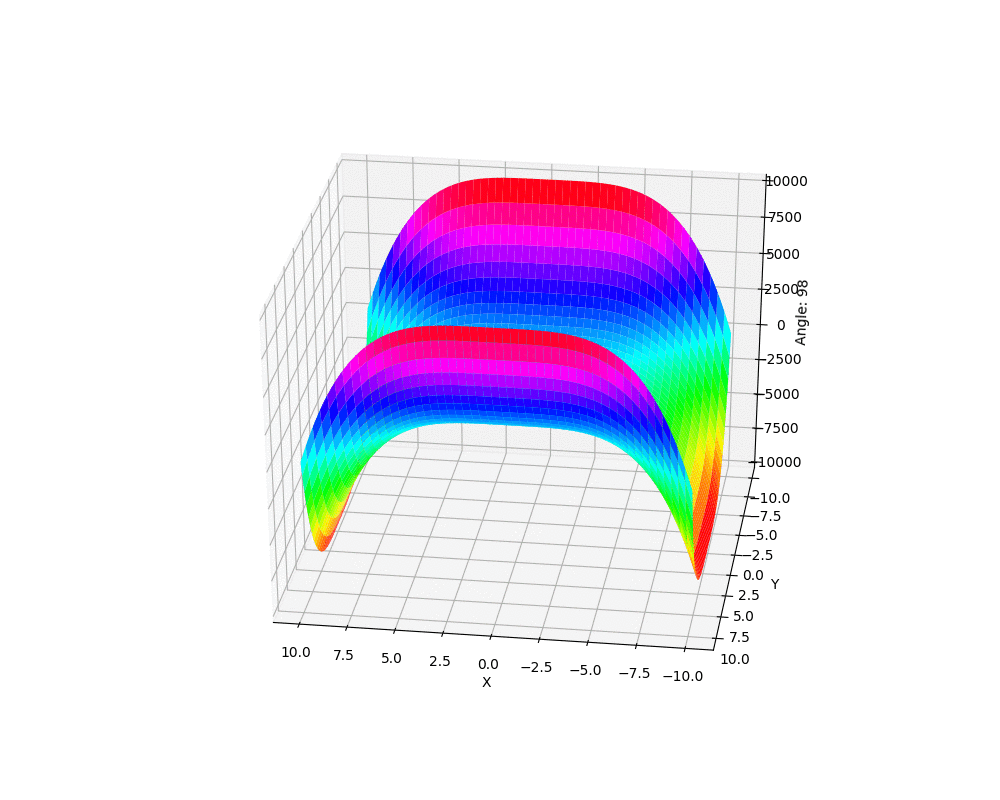
结束语
能够绘制3D图形将是一项非常有用的技能。因为在今后的机器学习过程中,我们常常会将数据以图形的形式展示出来,以便我们观察和了解。
由于篇幅所限,本文只介绍了一些最基本的用法,但实际上Matplotlib所支持的功能远不止这些,因此建议读者朋友们以此为基础继续进行更多的探索。
参考资料与推荐读物
- Matplotlib官方网站
- mplot3d tutorial
- 3D - The Python Graph Gallery
- Three-Dimensional Plotting in Matplotlib
原文地址:《使用Matplotlib绘制3D图形》 by 保罗的酒吧
