hector算法核心--高斯牛顿详解
基础知识
条件概率公式
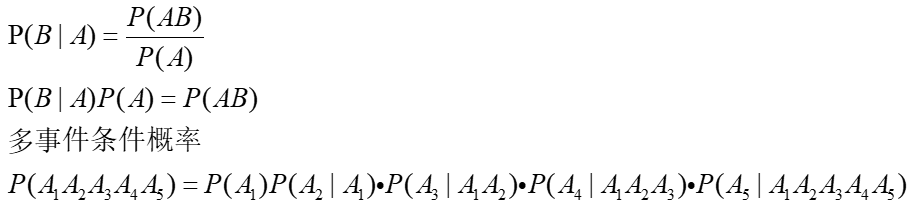
拉格朗日中值定理
如果函数f(x)在闭区间上[a,b]连续,在开区间(a,b)上可导,那么在开区间(a,b)内至少存在一点ξ使得f'(ξ)=(f(b)-f(a))/(b-a),它反映了可导函数在闭区间上的整体的平均变化率与区间内某点的局部变化率的关系
柯西中值定理
柯西中值定理是拉格朗日中值定理的推广,是微分学的基本定理之一。其几何意义为,用参数方程表示的曲线上至少有一点,它的切线平行于两端点所在的弦。该定理可以视作在参数方程下拉格朗日中值定理的表达形式。

泰勒中值定理


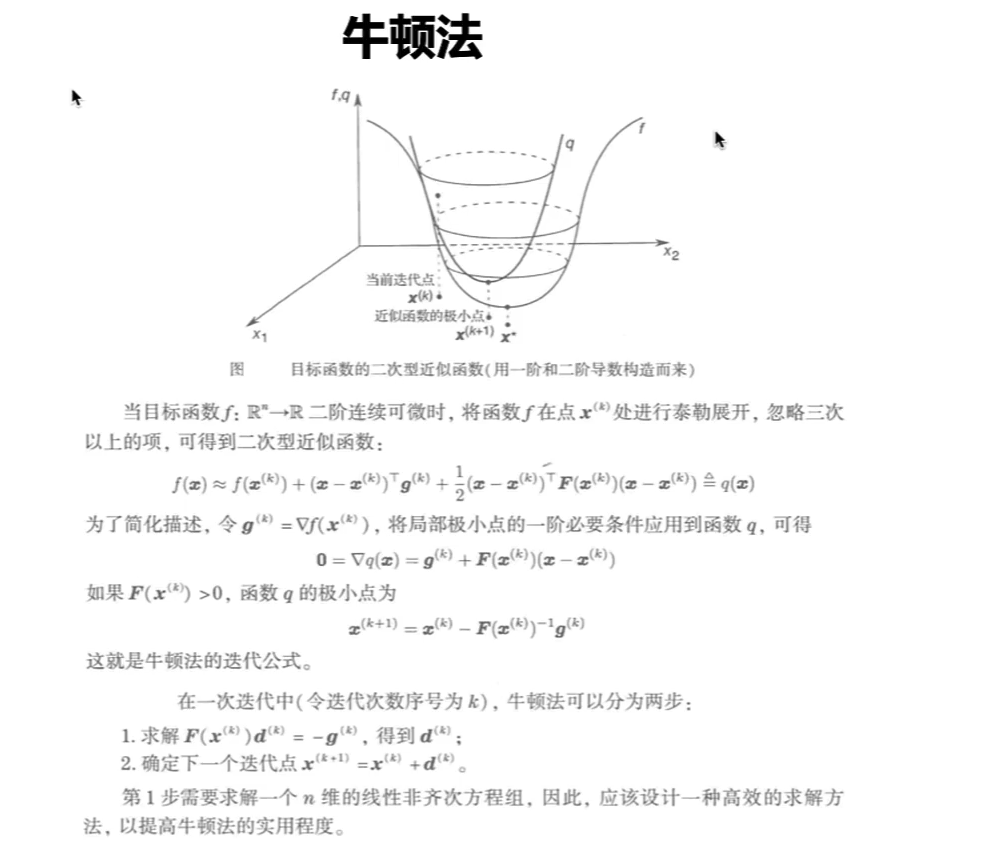


牛顿法
缺点:
- 距离极小值点距离必须近
- 计算量比较大
牛顿-高斯法讲解

hector算法算法核心讲解--牛顿高斯法




手写推导


