电磁学相关该概念与含义

磁场强度B

磁感应强度（或称磁通密度）是描述磁场强度的一种物理量，通常用符号 $ \mathbf{B} $ 表示，其单位是特斯拉（Tesla，符号为 T）。磁感应强度可以用来描述磁场在某一点的强度和方向。它的定义是：

$\mathbf{B} = \frac{\Phi}{A} $

其中：

• $\mathbf{B} $ 是磁感应强度，
• $ \Phi$ 是通过面积 ( A ) 的磁通量，
• $ A $ 是垂直于磁场方向的面积。

在电磁学中，磁感应强度的另一个定义是通过洛伦兹力来描述的：

$ \mathbf{F} = q (\mathbf{v} \times \mathbf{B}) $

其中：

• $\mathbf{F} $ 是洛伦兹力，
• $ q $是带电粒子的电荷，
• $\mathbf{v} $是带电粒子的速度，
• $\mathbf{B}$是磁感应强度。

磁感应强度的方向通常用磁力线的方向表示，磁力线从磁体的北极出发，穿过空间，再回到磁体的南极。磁感应强度越大，磁力线越密集。

由于磁场中某点的磁场方向是确定的，所以磁场中的磁感线不会相交。

载流导线周围的磁感线都是围绕电流的闭合曲线，没有起点，也没有终点。

磁通量$ \Phi $

磁通量（Magnetic Flux）是描述磁场通过一定面积的总量，通常用符号$ \Phi $表示，其单位是韦伯（Weber，符号为 Wb）。磁通量可以理解为通过一个面（通常是一个封闭回路或线圈）的磁力线的总数。

磁通量的定义是：

$\Phi = \mathbf{B} \cdot \mathbf{A} $

或者更具体地，通过积分形式表示为：

$ \Phi = \int_{A} \mathbf{B} \cdot d\mathbf{A} $

其中：

• $ \Phi $是磁通量，
• $ \mathbf{B}$是磁感应强度（磁通密度），
• $ \mathbf{A} $是垂直于磁场方向的面积，
• $ d\mathbf{A} $ 是微小面积元。

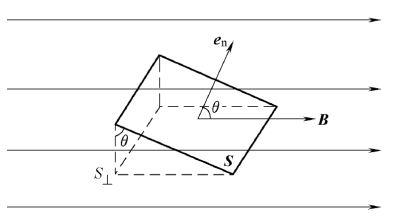
磁通量的大小不仅取决于磁感应强度$ \mathbf{B} $的大小，还取决于磁场方向与面积 $ \mathbf{A} $的夹角以及面积的大小。

举个例子，如果磁场 ( \mathbf{B} ) 垂直穿过一个面积为 ( A ) 的平面，则磁通量为：

$\Phi = B \cdot A $

如果磁场与面积成一定角度 ( \theta )，则磁通量为：

$ \Phi = B \cdot A \cdot \cos \theta$

磁通量在电磁学中的应用非常广泛，比如法拉第电磁感应定律就是基于磁通量变化来描述感应电动势的产生：

$ \mathcal{E} = -\frac{d\Phi}{dt}$

其中$ \mathcal{E} $是感应电动势， $ \frac{d\Phi}{dt} $ 是磁通量的时间变化率。

感应电动势$\mathcal{E} $

感应电动势（Electromotive Force, EMF）是指由于磁通量的变化在导体或电路中产生的电动势。

磁链 $\Psi $

磁链（磁通链）是指通过电感元件或线圈的磁通量总和。它反映了线圈中磁通量的总链接效应。

希腊字母 $\Psi $也常用来表示磁链（磁通链）。所以磁链的表达式可以写为：

$Ψ=NΦ $

其中：

• $\Psi $是磁链（磁通链），
• $N $ 是线圈的匝数，
• $\Phi $是每匝的磁通量（单位：韦伯，Wb）。

动生电动势$E$

动生电动势（Motional EMF）是指导体在磁场中运动时产生的电动势。根据法拉第电磁感应定律，导体运动导致其切割磁感线，从而产生感应电动势，称为动生电动势。

动生电动势的大小由以下公式决定：

$E = BLv sin(v, B)$

其中：

• $E$：动生电动势（单位：伏特，V）
• $B$：磁感强度（单位：特斯拉，T）
• $L$：导体长度（单位：米，m）
• $v$：导体运动速度（单位：米/秒，m/s）
• $(v, B)$：导体运动速度与磁感强度之间的夹角

动生电动势具有以下特点：

• 动生电动势的方向垂直于导体运动方向和磁场方向。
• 动生电动势的大小与导体长度、运动速度、磁感强度以及导体运动速度与磁场方向之间的夹角成正比。
• 动生电动势的产生不需要外部电源，是一种自感电动势。

感生电动势$E$

感生电动势（Induced electromotive force, EMF），又称感生电动势，是指导体在磁场中运动或磁场发生变化时，在导体中产生的电动势。根据法拉第电磁感应定律，感生电动势的大小与磁通量变化率成正比。

感生电动势的公式为：

$E = -nΔΦ/Δt$

其中：

• $E$：感生电动势（单位：伏特，V）
• $n$：导体匝数
• $ΔΦ$：磁通量变化量（单位：韦伯，Wb）
• $Δt$：时间变化量（单位：秒，s）

感生电动势具有以下特点：

• 感生电动势的方向与磁通量变化的方向相反。
• 感生电动势的大小与导体匝数、磁通量变化率成正比。
• 感生电动势的产生不需要外部电源，是一种自感电动势。

磁化强度（Magnetization）是指物质在外磁场作用下，其内部磁矩的平均值。它描述了材料被磁化的程度，表示单位体积内的净磁矩。磁化强度通常用符号 ( \mathbf{M} ) 表示，单位为安培每米（A/m）。

磁化强度$ \mathbf{M} $

磁化强度的定义

磁化强度 $\mathbf{M} $的定义为单位体积的净磁矩：

$ \mathbf{M} = \frac{\sum \mathbf{m}}{V} $

其中：

• $ \mathbf{M}$ 是磁化强度（单位：A/m），
• $\sum \mathbf{m} $是材料内所有磁矩的总和，
• $ V $ 是材料的体积。

磁化强度与外部磁场的关系

当材料放置在外部磁场$\mathbf{H} $ 中时，会产生磁化强度$ \mathbf{M} $。磁化强度 $\mathbf{M}$和外部磁场 $ \mathbf{H}$之间的关系通常用磁化率 $ \chi $来表示：

$\mathbf{M} = \chi \mathbf{H}$

其中：

• $ \chi $ 是磁化率，是无量纲量，
• $ \mathbf{H} $是外部磁场强度（单位：A/m）。

磁感应强度与磁化强度的关系

磁感应强度$ \mathbf{B}$ 与磁化强度$ \mathbf{M} $ 和外部磁场$ \mathbf{H} $的关系为：

$\mathbf{B} = \mu_0 (\mathbf{H} + \mathbf{M}) $

其中：

• $ \mathbf{B}$ 是磁感应强度（单位：特斯拉，T），
• $ \mu_0$ 是真空磁导率，值约为 $4\pi \times 10^{-7} $ H/m。

磁化强度的物理意义

磁化强度表示材料在外磁场作用下，内部磁矩的平均值。它反映了材料的磁性特征，表明材料在外磁场下磁化的能力。磁化强度的大小和方向与外磁场的大小和方向有关。

####例子：铁磁材料的磁化强度

对于铁磁材料，如铁和镍，在强外部磁场作用下，磁化强度 ( \mathbf{M} ) 会迅速增加并达到饱和状态。这是因为铁磁材料内的磁畴在外磁场作用下迅速对齐，产生强大的净磁矩。

$\mathbf{M} \approx M_s $

其中 ( M_s ) 是材料的饱和磁化强度。

总结来说，磁化强度是描述材料在外磁场作用下磁化程度的重要物理量，通过了解和应用磁化强度，可以更好地理解和利用材料的磁性特征。

磁场强度$ \mathbf{H} $

磁场强度（Magnetic Field Strength），也称磁场强度矢量，表示磁场的强度和方向。它通常用符号 $ \mathbf{H} $表示，单位为安培每米（A/m）。磁场强度是一个矢量量，描述了磁场在空间中任一点的性质。

磁场强度的定义

磁场强度 $ \mathbf{H} $ 的定义可以通过磁感应强度$ \mathbf{B} $ 和磁化强度 $\mathbf{M} $表示：

$ \mathbf{H} = \frac{\mathbf{B}}{\mu_0} - \mathbf{M}$

其中：

• $ \mathbf{H} $是磁场强度（单位：A/m），
• $ \mathbf{B} $ 是磁感应强度（单位：特斯拉，T），
• $\mu_0 $ 是真空磁导率，值约为 $ 4\pi \times 10^{-7} $ H/m，
• $ \mathbf{M} $ 是磁化强度（单位：A/m）。

在真空或非磁化物质中（即$ \mathbf{M} = 0 $）：

$ \mathbf{H} = \frac{\mathbf{B}}{\mu_0} $

磁场强度的物理意义

磁场强度 $ \mathbf{H} $ 表示磁场源的强度，与磁场的产生有关。在电磁学中，磁场强度通常与电流和磁性物质的磁化有关。

磁场强度与磁化强度的关系

在有磁性的材料中，磁场强度与磁化强度之间存在以下关系：

$\mathbf{B} = \mu_0 (\mathbf{H} + \mathbf{M}) $

其中：

• $ \mathbf{B} $ 是磁感应强度，
• $ \mathbf{H} $是磁场强度，
• $ \mathbf{M} $是磁化强度，
• $ \mu_0$ 是真空磁导率。

安培环路定理

安培环路定理描述了磁场强度和电流之间的关系。对于任意闭合路径，磁场强度 $ \mathbf{H} $沿路径的线积分等于路径所包围的电流总和：

$ \oint_{\partial S} \mathbf{H} \cdot d\mathbf{l} = I_{\text{enc}} $

其中：

• $\oint_{\partial S} \mathbf{H} \cdot d\mathbf{l}$是磁场强度沿闭合路径的线积分，
• $ I_{\text{enc}}$是路径所包围的总电流。

应用

1. 电磁铁：在电磁铁中，通过控制线圈中的电流，可以调整磁场强度，从而控制电磁铁的磁力。
2. 磁性材料：在磁性材料的研究中，磁场强度 $ \mathbf{H}$是一个重要的参数，用于描述材料在外磁场中的响应。
3. 电动机和发电机：磁场强度在电动机和发电机的设计中至关重要，决定了设备的性能和效率。

例子：长直导线的磁场强度

对于一根无限长直导线，载流 $I $的磁场强度 $\mathbf{H} $ 在距离导线$ r $ 处的表达式为：

$ H = \frac{I}{2\pi r} $

这是由安培环路定理推导出来的结果。

磁导率$ \mu $

磁导率（Magnetic Permeability）是物质在磁场中被磁化的程度的量度。它表示磁感应强度$ \mathbf{B} $ 与磁场强度 $ \mathbf{H}$ 之间的关系。磁导率通常用符号 $ \mu $ 表示，单位为亨利每米（H/m）或牛顿每安培平方（N/A²)。

磁导率的定义

磁导率$ \mu$定义为磁感应强度 $\mathbf{B} $与磁场强度 $ \mathbf{H} $之比：

$ \mathbf{B} = \mu \mathbf{H} $

其中：

• $ \mathbf{B} $是磁感应强度（单位：特斯拉，T），
• $\mathbf{H} $ 是磁场强度（单位：安培每米，A/m），
• $ \mu $是磁导率（单位：H/m 或 N/A²）。

真空磁导率和相对磁导率

1. 真空磁导率（Vacuum Permeability）：也称为磁常数，用符号 $ \mu_0$ 表示。它是自由空间的磁导率，数值约为 $ 4\pi \times 10^{-7} $H/m。

$ \mu_0 \approx 4\pi \times 10^{-7} , \text{H/m} $

2. 相对磁导率（Relative Permeability）：表示物质的磁导率与真空磁导率的比值，用符号 $ \mu_r $表示。相对磁导率是无量纲量。

$ \mu_r = \frac{\mu}{\mu_0} $

其中：

• $ \mu $是材料的磁导率，
• $ \mu_0 $ 是真空磁导率，
• $ \mu_r $是相对磁导率。

磁导率的分类

1. 顺磁材料（Paramagnetic Materials）：顺磁材料的相对磁导率 $ \mu_r $略大于 1。这些材料在外磁场作用下会被微弱地磁化。

2. 抗磁材料（Diamagnetic Materials）：抗磁材料的相对磁导率 $ \mu_r $ 略小于 1。这些材料在外磁场作用下会微弱地产生与磁场方向相反的磁化。

3. 铁磁材料（Ferromagnetic Materials）：铁磁材料的相对磁导率 $ \mu_r $很大，通常在几百到几千范围内。这些材料在外磁场作用下会被强烈磁化。

磁滞回线

磁滞回线描述了磁性材料在外磁场作用下磁化强度 $ \mathbf{M} $或磁感应强度 $ \mathbf{B} $与磁场强度$\mathbf{H}$ 之间的关系。这条曲线反映了磁性材料的磁滞现象，即当外磁场变化时，材料的磁化状态并不立即响应，而是存在一定的滞后效应。

磁滞回线的绘制

磁滞回线通常绘制为磁感应强度 $ \mathbf{B} $ 对磁场强度$\mathbf{H}$ 的图，或磁化强度$ \mathbf{M}$ 对磁场强度 $ \mathbf{H} $的图。

磁感应强度 $ \mathbf{B} $ 与磁场强度 $ \mathbf{H} $ 的磁滞回线

1. 初始磁化曲线：当外磁场 $ \mathbf{H} $ 从零开始增加时，磁感应强度 $ \mathbf{B} $逐渐增加，直到达到饱和磁感应强度 $B_s $。

2. 磁化曲线：当 $ \mathbf{H} $ 达到一定值后开始减小，$\mathbf{B}$也减小，但并不回到零，而是达到一个剩磁 $B_r$的值，这说明材料在没有外磁场时仍保留一定的磁性。

3. 去磁曲线：继续反向增加 $\mathbf{H}$，直到$\mathbf{B} $ 变为零，此时的磁场强度称为矫顽力 $ H_c $。

4. 反向磁化曲线：反向继续增加$ \mathbf{H} $，$\mathbf{B}$ 达到反向饱和磁感应强度 $ -B_s$。

5. 闭合回线：反向减少 $ \mathbf{H} $，再反向增加，形成闭合的磁滞回线。

磁滞回线的特性

1. 饱和磁感应强度（Saturation Magnetic Induction） $ B_s $：在强外磁场下，磁感应强度达到最大值。

2. 剩磁（Remanence） $B_r $：外磁场 ( \mathbf{H} ) 回到零时，材料中残留的磁感应强度。

3. 矫顽力（Coercivity） $ H_c $：使磁感应强度$ \mathbf{B} $ 回到零所需施加的反向磁场强度。

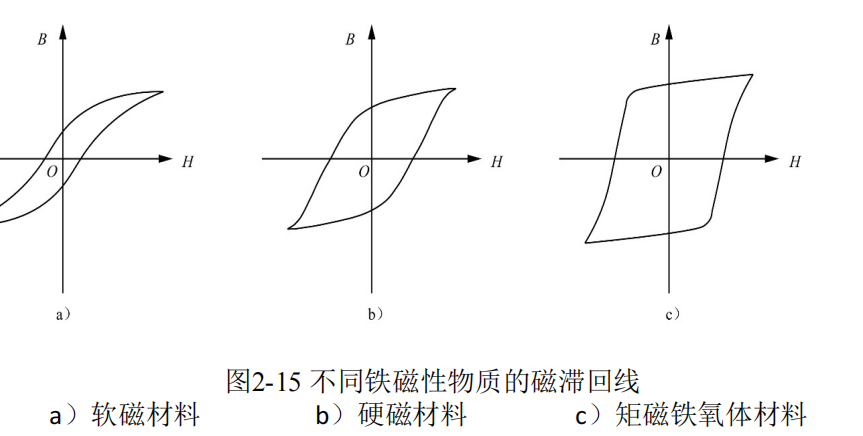
例子：软磁材料与硬磁材料的磁滞回线

1. 软磁材料：如铁、镍，磁滞回线较窄，矫顽力 $ H_c $小，容易磁化和去磁化，适用于变压器和电感元件。

2. 硬磁材料：如钕铁硼，磁滞回线较宽，矫顽力$ H_c $大，难以去磁，适用于永久磁铁和磁存储设备。

磁路

磁路（Magnetic Circuit）是用来描述磁场在磁性材料中路径的模型，类似于电路用于描述电流在导体中的路径。

主磁通$\Phi_m $

主磁通（Main Magnetic Flux）通常用符号 $\Phi_m $ 表示，指在磁路中主要路径上流动的磁通量，它在电磁设备的工作中起到主要作用。磁通的大小与设备的磁动势和磁路的磁导率等因素有关。

主磁通的计算

主磁通可以通过以下公式计算：

$ \Phi_m = \frac{\mathcal{F}}{\mathcal{R}} $

其中：

• $ \Phi_m $ 是主磁通（单位：韦伯，Wb），
• $ \mathcal{F} $ 是磁动势（单位：安培，A），
• $ \mathcal{R} $ 是磁路的磁阻（单位：安培每韦伯，A/Wb）。

漏磁通 $ \Phi_l $

漏磁通（Leakage Flux）通常用符号 $ \Phi_l $ 表示，指在磁路中不通过预定路径或工作区域的磁通量。与主磁通不同，漏磁通绕过主要磁性材料或工作区域，可能会导致设备性能下降或效率降低。

漏磁通的影响

漏磁通会导致以下几个方面的影响：

1. 降低效率：漏磁通不参与有效的能量转换或传输，导致能量损失。
2. 增加电感：在变压器或电动机中，漏磁通增加了漏电感，影响设备的性能。
3. 产生不必要的热量：漏磁通在非工作区域中可能产生不必要的热量，影响设备的散热和寿命。

洛伦兹力和安培力

洛伦兹力和安培力都是描述带电粒子和电流在磁场中受到的力的概念，但它们有不同的应用范围和定义方式。以下是它们的详细介绍：

洛伦兹力

洛伦兹力（Lorentz Force）是描述带电粒子在电场和磁场中所受的总力。其数学表达式为：

$\mathbf{F} = q(\mathbf{E} + \mathbf{v} \times \mathbf{B}) $

其中：

• $ \mathbf{F} $是带电粒子受到的总力，
• $q $是带电粒子的电荷，
• $ \mathbf{E} $是电场强度，
• $ \mathbf{v} $ 是带电粒子的速度，
• $ \mathbf{B} $ 是磁感应强度（磁场）。

洛伦兹力可以分为两个部分：

1. 电场力 $ \mathbf{F}_E = q\mathbf{E}$
2. 磁场力$ \mathbf{F}_B = q(\mathbf{v} \times \mathbf{B}) $

其中，磁场力的方向由右手定则确定，即如果右手的拇指指向带电粒子的速度方向，四指指向磁场方向，则磁场力的方向垂直于这两个方向。

安培力

安培力（Ampère Force）是描述载流导线在磁场中受到的力。其数学表达式为：

$ d\mathbf{F} = I (d\mathbf{l} \times \mathbf{B}) $

其中：

• $ d\mathbf{F} $是导线微小段$ d\mathbf{l} $ 所受的力，
• $ I $ 是导线中的电流，
• $ d\mathbf{l} $是导线微小段的长度向量，
• $ \mathbf{B} $ 是磁感应强度（磁场）。

对于一段长度为 $ L $ 的直导线，其受力可以写成：

$ \mathbf{F} = I (\mathbf{L} \times \mathbf{B})$

同样，安培力的方向也由右手定则确定，即如果右手的拇指指向电流方向，四指指向磁场方向，则安培力的方向垂直于这两个方向。

比较与联系

• 作用对象：洛伦兹力作用于单个带电粒子，而安培力作用于载流导线。
• 来源：洛伦兹力包含电场力和磁场力两部分，而安培力仅考虑磁场对载流导线的作用。
• 表达式：洛伦兹力公式中包含电场和磁场项，而安培力公式中仅包含磁场项。

磁动势$ \mathcal{F} $

磁动势（Magnetomotive Force, MMF）是磁场驱动磁通量在磁路中流动的“推动力”，类似于电路中的电动势。磁动势是磁路分析的关键概念之一。

磁动势的定义

• 磁动势 $ \mathcal{F} $ 是驱动磁通量 $ \Phi $ 在磁路中流动的“推动力”，其计算公式为：

  $ \mathcal{F} = N I $

  其中：

  • $ N $ 是线圈的匝数，
  • $ I $ 是通过线圈的电流（单位：安培，A）。

磁动势表示通过一个磁环或磁路的线圈产生的总磁动势。

磁动势的物理意义

磁动势在磁路中起到类似于电动势在电路中的作用，驱动磁通量 ( \Phi ) 在磁路中流动。磁动势的大小决定了磁场的强度和磁通量的多少。

磁动势与磁通量的关系

磁动势与磁通量的关系通过磁阻表达：

$ \Phi = \frac{\mathcal{F}}{\mathcal{R}} $

其中：

• $\Phi$ 是磁通量（单位：韦伯，Wb），
• $ \mathcal{F} $是磁动势（单位：安培，A），
• $ \mathcal{R} $是磁阻（单位：安培每韦伯，A/Wb）。

磁阻$ \mathcal{R} $

磁阻（Magnetic Reluctance）是描述磁性材料或磁路对磁通量的阻碍程度的量度，类似于电阻在电路中的作用。它表征了磁通量在磁路中流动的难易程度。

磁阻的定义

磁阻定义为：

$ \mathcal{R} = \frac{l}{\mu A} $

其中：

• $ \mathcal{R} $ 是磁阻（单位：安培每韦伯，A/Wb），
• $ l $ 是磁路的长度（单位：米，m），
• $ \mu $ 是磁导率（单位：亨利每米，H/m），
• $ A $ 是磁路的横截面积（单位：平方米，m²）。

####磁阻的物理意义

磁阻表示磁场在磁路中遇到的阻碍。磁阻越大，磁场在磁路中流动的难度就越大。磁阻的大小取决于磁路的几何尺寸（长度和截面积）以及材料的磁导率。

####磁阻与磁动势和磁通量的关系

通过安培环路定律，磁阻与磁动势和磁通量之间的关系可以表示为：

$ \mathcal{F} = \Phi \mathcal{R} $

其中：

• $ \mathcal{F} $ 是磁动势（单位：安培，A），
• $ \Phi $ 是磁通量（单位：韦伯，Wb），
• $ \mathcal{R}$ 是磁阻（单位：安培每韦伯，A/Wb）。

磁阻的影响因素

1. 磁路的长度：磁路长度越长，磁阻越大。增加磁路的长度会增加磁通量的阻碍。

2. 磁路的横截面积：磁路的横截面积越大，磁阻越小。增加横截面积可以降低磁通量的阻碍。

3. 磁导率：材料的磁导率 ( \mu ) 越高，磁阻越小。磁导率表示材料对磁场的导磁能力，高磁导率材料有助于降低磁阻。

了解了，如果你想用符号 ( \wedge ) 来表示磁导（Magnetic Conductance），那么可以这样定义：

磁导$ \wedge $

磁导 $ \wedge $ 是描述磁性材料或磁路对磁通量传导能力的量度，类似于电导在电路中的作用。磁导的定义为：

$ \wedge = \frac{\mu A}{l} $

其中：

• $ \wedge $是磁导（单位：亨利每米每安培，H/m/A），
• $ \mu $ 是材料的磁导率（单位：亨利每米，H/m），
• $ A $ 是磁路的横截面积（单位：平方米，m²），
• $ l $ 是磁路的长度（单位：米，m）。

磁导与磁阻的关系

磁导和磁阻之间的关系可以表示为：

$ \wedge = \frac{1}{\mathcal{R}} $

其中：

• $ \mathcal{R} $是磁阻（单位：安培每韦伯，A/Wb）。

励磁磁通（Excitation Flux）是指在电磁设备中（如发电机、电动机）的励磁系统中产生的磁通量。它主要由励磁绕组或励磁系统产生，是维持设备正常运行的关键因素之一。以下是励磁磁通的详细解释：

励磁磁通$ \Phi_f $

励磁磁通是由励磁绕组中的电流产生的磁通量。在发电机或电动机中，励磁绕组（通常称为励磁机或励磁绕组）通过直流电流产生一个稳定的磁场，这个磁场形成的磁通量被称为励磁磁通。

励磁磁通的产生

励磁磁通由励磁绕组中的电流产生，这些绕组通常是连接在电机的转子部分或静止部分（根据电机的类型）。励磁电流通过绕组产生一个稳定的磁场，磁场的强度决定了励磁磁通的大小。

数学表达

励磁磁通$ \Phi_f $ 可以表示为：

$ \Phi_f = B \cdot A $

其中：

• $ B $ 是磁感应强度（单位：特斯拉，T），
• $ A $ 是磁通穿过的面积（单位：平方米，m²）。

此外，励磁磁通也可以与励磁电流 $ I_f $和励磁绕组的匝数 $N $ 相关联：

$ \Phi_f = \frac{L_f \cdot I_f}{N} $

其中：

• $ L_f $ 是励磁绕组的磁感应系数（单位：亨利，H），
• $I_f $ 是励磁电流（单位：安培，A），
• $ N $ 是励磁绕组的匝数。

励磁电感$ L_m $

励磁电感（Magnetizing Inductance）是指电力变压器或电动机的励磁绕组在通电后产生的电感。励磁电感表示在励磁电流作用下，绕组产生磁通量的能力。它可以看作是设备中用于建立和维持磁场的部分电感。励磁电感反映了设备产生和维持磁场的能力，是变压器和电动机设计中一个重要参数。

励磁电感的数学表达

励磁电感 $ L_m $ 通常通过如下公式定义：

$ L_m = \frac{N^2 \mu A}{l} $

其中：

• $ L_m $ 是励磁电感（单位：亨利，H），
• $ N $ 是绕组的匝数，
• $ \mu $ 是磁芯的磁导率（磁导率和磁导不同，磁导率是材料特性）,
• $ A $ 是磁芯的截面积（单位：平方米，m²），
• $ l $是磁路的长度（单位：米，m）。

励磁电感在变压器中的作用

在变压器中，励磁电感主要与变压器的初级绕组相关。当变压器的次级绕组无负载时，初级绕组中的励磁电流通过励磁电感来产生必要的磁场。这些磁场在铁芯中形成磁通，进而在次级绕组中感应出电动势。

励磁电感的特性

1. 空载条件：在变压器或电动机空载时，励磁电感是主要的电感成分。它决定了空载电流的大小。
2. 磁芯特性：励磁电感与磁芯材料和结构紧密相关。高磁导率的磁芯材料可以显著提高励磁电感。
3. 线圈匝数：匝数越多，励磁电感越大，但匝数增加也会增加线圈的电阻和制造复杂性。
4. 频率依赖性：励磁电感通常会随频率变化。在高频应用中，励磁电感的有效值可能会降低。

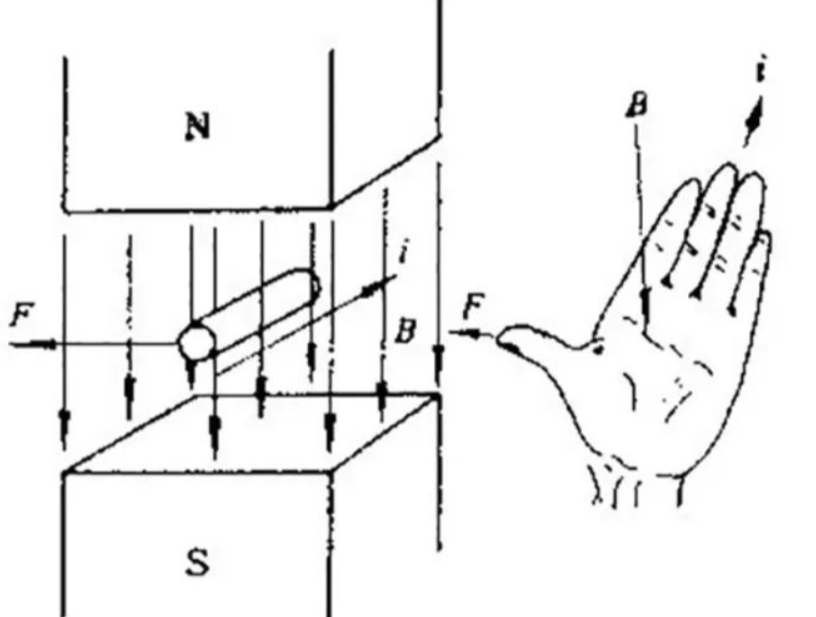
左手定则

用于判断导线在磁场中受力的方向：伸开左手，使拇指与其他四指垂直且在一个平面内，让磁感线从手心流入，四指指向电流方向，大拇指指向的就是安培力方向（即导体受力方向）。

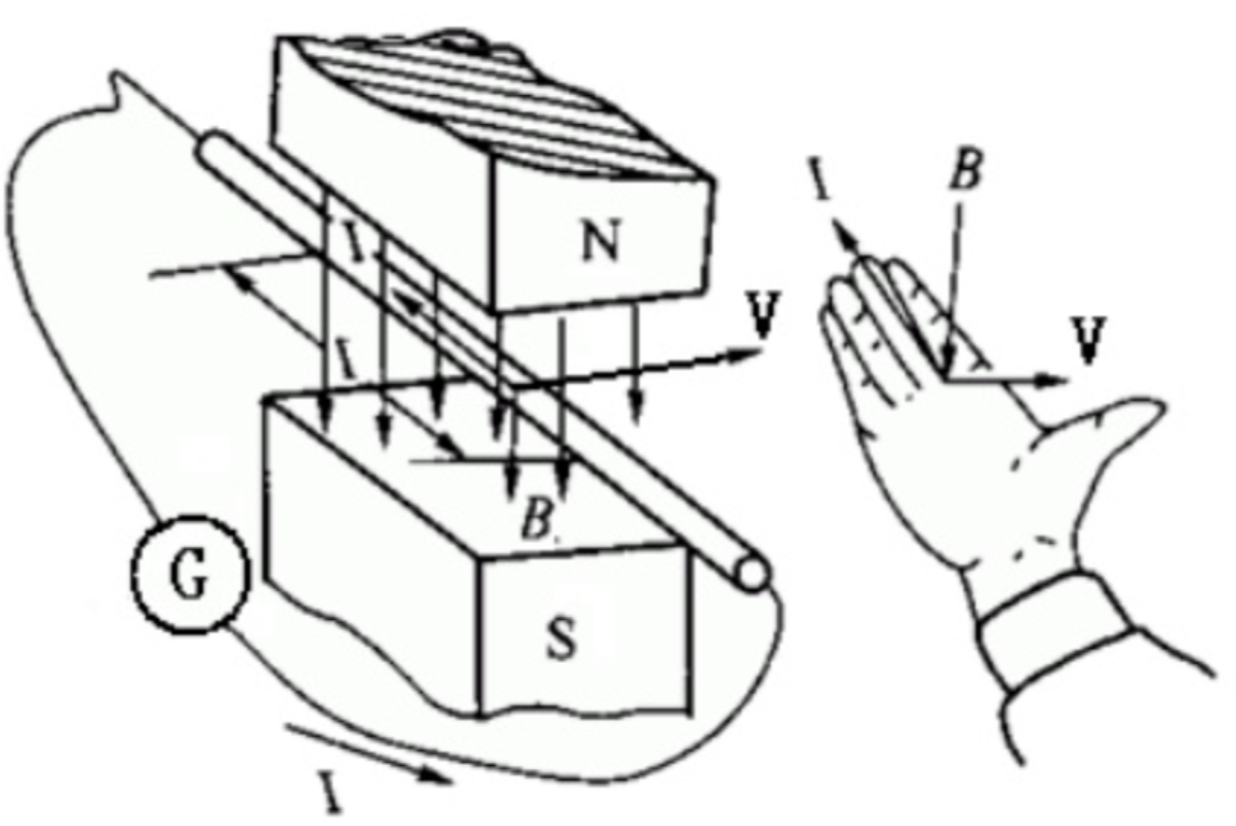
右手定则

伸开右手，使大拇指跟其余四个手指垂直并且都跟手掌在一个平面内，把右手放入磁场中，让磁感线垂直穿入手心，大拇指指向导体运动方向，则其余四指指向感生电动势的方向。也就是切割磁感线的导体会产生反电动势，实际上通过反电动势定位转子位置也是普通无感电调工作的基础原理之一。

右手螺旋定则（即安培定则）

用于判断通电线圈判断极性：用右手握螺线管，让四指弯向螺线管中电流方向，大拇指所指的那端就是螺线管的N极。直线电流的磁场的话，大拇指指向电流方向，另外四指弯曲指的方向为磁感线的方向。

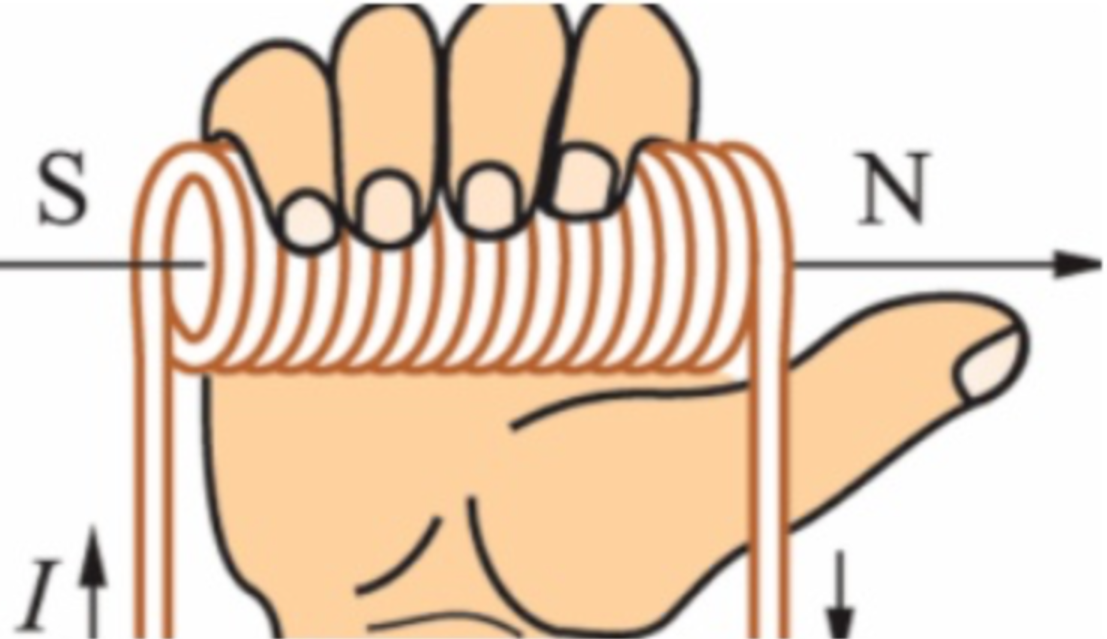
高斯定理/磁通连续性定理

由于磁感线是闭合的，因此对任一闭合曲面来说，有多少条磁感线进入闭合曲面，就一定有多少条磁感线穿出闭合曲面。也就是说，通过任意闭合曲面的磁通量必等于零。

毕奥-萨伐尔定律

毕奥-萨伐尔定律（Biot-Savart Law）是描述电流产生磁场的一个基本定律。它可以用来计算任意形状的载流导线在空间中某一点产生的磁感应强度（磁场）。

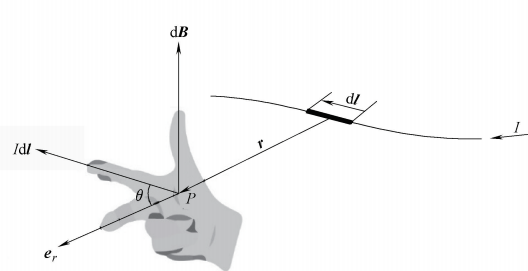
毕奥-萨伐尔定律的数学表达式为：

$d\mathbf{B} = \frac{\mu_0}{4\pi} \frac{I , d\mathbf{l} \times \mathbf{r}}{r^3} $

其中：

• $ d\mathbf{B} $ 是电流元 $ I , d\mathbf{l} $ 在距离 $\mathbf{r} $ 处产生的微小磁感应强度，
• $ \mu_0 $ 是真空磁导率，约为$ 4\pi \times 10^{-7} , \text{H/m} $（亨利每米），
• $ I $ 是电流强度，
• $ d\mathbf{l} $是电流元的微小长度向量，
• $ \mathbf{r} $ 是从电流元指向观察点的矢量，
• $ r $ 是 $\mathbf{r} $ 的模，即 $r = |\mathbf{r}|$。

毕奥-萨伐尔定律表示，电流元 $ I , d\mathbf{l} $在距离$r $处产生的磁场$ d\mathbf{B}$ 的大小与电流强度 I$ $和电流元的长度成正比，与 $ r $ 的平方成反比，并且磁场方向由右手螺旋定则确定。

对一段导线上的所有电流元积分，可以得到该导线在空间中任意一点产生的总磁感应强度 $ \mathbf{B} $

$ \mathbf{B} = \frac{\mu_0}{4\pi} \int \frac{I , d\mathbf{l} \times \mathbf{r}}{r^3} $

这条定律在计算复杂电流分布产生的磁场时非常有用，例如计算圆环电流、直导线和螺线管等的磁场分布。

安培环路定理

安培环路定理（Ampère's Circuital Law）是电磁学中描述磁场与电流之间关系的基本定律之一。它指出，磁场沿闭合路径的环量等于该路径所包围的电流总和乘以真空磁导率。数学表达式为：

$ \oint_{\partial \Sigma} \mathbf{B} \cdot d\mathbf{l} = \mu_0 I_{\text{enc}} $

其中：

• $ \oint_{\partial \Sigma} \mathbf{B} \cdot d\mathbf{l} $是沿闭合路径$\partial \Sigma $ 的磁场$\mathbf{B} $的环量（线积分），
• $ \mu_0 $ 是真空磁导率，约为$ 4\pi \times 10^{-7} , \text{H/m} $（亨利每米），
• $ I_{\text{enc}} $ 是路径 $\partial \Sigma $ 所包围的净电流。

安培环路定理的一个常见应用是计算具有对称性的电流分布产生的磁场。例如，在无限长直导线和螺线管等情况下，可以方便地使用安培环路定理来求解磁场。

例子：无限长直导线的磁场

对于一根无限长直导线，电流 ( I ) 沿导线流动。我们选择一个以导线为轴心、半径为 ( r ) 的圆形安培环路。

根据安培环路定理：

$ \oint_{\partial \Sigma} \mathbf{B} \cdot d\mathbf{l} = \mu_0 I $

由于磁场$\mathbf{B} $ 在环路上的每一点都是相同的（因为对称性）并且方向与环路切线方向一致，我们有：

$ B \cdot (2\pi r) = \mu_0 I $

因此，可以解出磁场强度 $ B $：

$ B = \frac{\mu_0 I}{2\pi r} $

这表示在距离无限长直导线$ r $处的磁场强度$ B $与电流 $ I $成正比，与距离 $ r $成反比。

麦克斯韦修正

麦克斯韦在安培环路定理中加入了位移电流密度，使其在更广泛的情况下适用。这一修正后的形式为：

$ \oint_{\partial \Sigma} \mathbf{B} \cdot d\mathbf{l} = \mu_0 (I_{\text{enc}} + \epsilon_0 \frac{d\Phi_E}{dt}) $

其中：

• $ \epsilon_0 $ 是真空电容率，
• $ \frac{d\Phi_E}{dt} $是电场通量随时间的变化率（位移电流密度）。

这一修正是麦克斯韦方程组的一部分，完善了电磁学理论。

磁路的安培环路定律

磁路的安培环路定律是描述磁场在闭合路径上磁场强度（$\mathbf{H} $ ）的总和等于该路径所包围的电流总和的定律。这一定律是磁路理论的基础之一，与电路中的基尔霍夫电压定律类似。

安培环路定律的数学表达式

安培环路定律的数学表达式为：

$ \oint_{\partial S} \mathbf{H} \cdot d\mathbf{l} = I_{\text{enc}} $

其中：

• $ \oint_{\partial S} \mathbf{H} \cdot d\mathbf{l} $ 是磁场强度 ( \mathbf{H} ) 沿闭合路径$ \partial S $ 的线积分，
• $ I_{\text{enc}} $ 是路径所包围的总电流。

应用于磁路

在磁路中，安培环路定律用于计算磁动势（MMF）和磁阻的关系，从而确定磁通量。磁路中的基本公式可以通过安培环路定律推导出来。

磁路中的欧姆定律

通过安培环路定律，可以得出磁路中的欧姆定律，即磁动势、磁通量和磁阻之间的关系：

$ \mathcal{F} = \Phi \mathcal{R} $

其中：

• $ \mathcal{F} $ 是磁动势（单位：安培，A），
• $ \Phi $ 是磁通量（单位：韦伯，Wb），
• $ \mathcal{R} $ 是磁阻（单位：安培每韦伯，A/Wb）。

例子：环形磁芯中的磁通量计算

考虑一个环形磁芯，线圈绕在磁芯上，有 $ N$ 匝，通过电流$ I$ 。环形磁芯的平均长度为 $ l $ ，截面积为 $ A $ ，磁导率为 $ \mu $ 。

1. 计算磁动势：

$ \mathcal{F} = N I $

2. 计算磁阻：

$ \mathcal{R} = \frac{l}{\mu A} $

3. 计算磁通量：

$ \Phi = \frac{\mathcal{F}}{\mathcal{R}} = \frac{N I}{\frac{l}{\mu A}} = \frac{N I \mu A}{l} $

楞次定律和法拉第电磁感应定律

楞次定律和法拉第电磁感应定律是电磁学中的两个重要定律，它们描述了磁通量变化和感应电动势之间的关系，并且二者密切相关。以下是它们的详细介绍和联系：

法拉第电磁感应定律

法拉第电磁感应定律描述了磁通量变化如何在电路中产生感应电动势（电压）。其数学表达式为：

$\mathcal{E} = -\frac{d\Phi}{dt} $

其中：

• $\mathcal{E} $ 是感应电动势（电压），
• $ \Phi $ 是通过电路的磁通量，
• $ \frac{d\Phi}{dt} $是磁通量随时间的变化率。

法拉第电磁感应定律指出，当磁通量随时间变化时，会在电路中产生一个感应电动势。这个感应电动势的大小与磁通量的变化率成正比，方向则由楞次定律决定。

楞次定律

楞次定律（Lenz's Law）描述了感应电动势的方向。它指出：感应电动势总是产生一个电流，其产生的磁场方向总是反抗原来磁通量的变化。这一定律可以用来确定法拉第电磁感应定律中负号的物理意义。

楞次定律可以表述为：

• 当磁通量增加时，感应电动势产生的磁场将试图减小磁通量。
• 当磁通量减小时，感应电动势产生的磁场将试图增加磁通量。

联系与综合

法拉第电磁感应定律给出了感应电动势的大小，而楞次定律给出了感应电动势的方向。结合这两个定律，可以完全描述感应电动势的行为。

示例：直导线穿过磁场

假设一根导线在磁场中移动，磁场方向垂直于导线的运动方向。根据法拉第电磁感应定律，导线中的感应电动势为：

$ \mathcal{E} = -\frac{d\Phi}{dt} $

如果磁通量增加，根据楞次定律，导线中的感应电动势会产生一个电流，该电流的磁场将反对磁通量的增加。如果磁通量减小，感应电动势产生的电流磁场将试图增加磁通量。

磁路的基尔霍夫第一定律是磁场分析中的一个基本原理，它类似于电路中基尔霍夫电流定律（KCL）。磁路中的基尔霍夫第一定律描述了磁通量在磁路节点的行为。

磁路的基尔霍夫第一定律

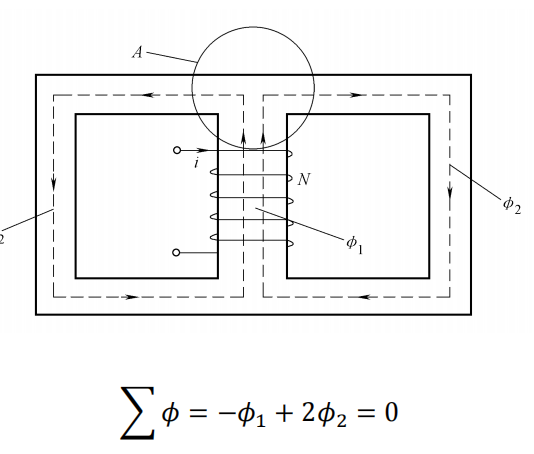
磁路的基尔霍夫第一定律表明，在磁路的任何一个节点（也称为磁节点或磁接点），流入节点的磁通量总和等于流出节点的磁通量总和。用数学公式表示为：

$ \sum_{k=1}^{n} \Phi_k = 0 $

其中：

• $ \Phi_k $ 是通过节点的第 ( k ) 条磁通量（单位：韦伯，Wb），
• $ n $ 是通过节点的磁通量数量。

物理意义

这个定律基于磁通量守恒原理，即磁通量不能在磁路的任何节点上被消失或产生。所有流入节点的磁通量必须等于所有流出节点的磁通量，从而确保了磁通量的守恒。

应用

1. 磁路分析：磁路的基尔霍夫第一定律用于计算磁通量在复杂磁路中的分布。例如，在分析铁芯中的磁场时，可以利用这个定律来建立磁通量平衡方程，从而求解磁场的分布情况。

2. 磁场设计：在磁性设备的设计中（如变压器、电动机），基尔霍夫第一定律帮助分析和优化磁路的磁通量分布，以提高设备的性能和效率。

例子

假设一个磁路有一个节点，节点处有三个磁通量分支：磁通量 $ \Phi_1 $ 流入节点，磁通量 $ \Phi_2 $和 $ \Phi_3 $ 流出节点。根据磁路的基尔霍夫第一定律：

$ \Phi_1 = \Phi_2 + \Phi_3 $

如果已知 $ \Phi_1 $ 的值和 $\Phi_2 $的值，可以通过上述公式计算 $ \Phi_3 $的值，反之亦然。

磁路的基尔霍夫第二定律类似于电路中的基尔霍夫电压定律（KVL），描述了磁路中磁动势（磁场强度）和磁通量之间的关系。具体来说，它涉及到沿着闭合磁路环路的磁动势和磁通量的关系。

磁路的基尔霍夫第二定律

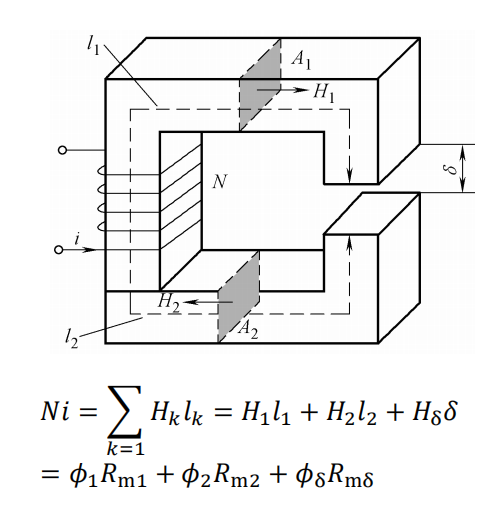
磁路的基尔霍夫第二定律表明，在磁路的任何闭合回路中，沿着回路的磁动势总和等于磁通量的变化总和。用数学公式表示为：

$ \sum_{k=1}^{n} \mathcal{F}k = \sum{k=1}^{n} \Phi_k $

其中：

• $ \mathcal{F}_k $ 是回路中第 $ k $ 条磁动势（单位：安培匝，A·turns），
• $ \Phi_k $ 是回路中第 $ k $ 条磁通量（单位：韦伯，Wb），
• $ n $ 是回路中磁动势和磁通量的数量。

物理意义

这个定律基于磁动势和磁通量之间的关系。它表明，在一个闭合磁路回路中，磁动势的代数和等于磁通量的变化总和。这反映了磁能在磁路中的分布和转换。

应用

1. 磁路分析：磁路的基尔霍夫第二定律用于计算磁路中磁动势的分布。通过应用这个定律，可以建立磁路的平衡方程，从而分析磁场和磁通量的分布。

2. 电磁设备设计：在设计变压器、电动机和发电机等电磁设备时，基尔霍夫第二定律帮助分析和优化磁路的磁动势分布，以提高设备的性能和效率。

例子

假设一个磁路有一个闭合回路，其中有两个磁动势源（$ \mathcal{F}_1$ 和 ( \mathcal{F}_2 )）和两个磁阻（( \mathcal{R}_1 ) 和 ( \mathcal{R}_2 )），磁通量通过这些元件。根据磁路的基尔霍夫第二定律，在回路中沿着任意方向（顺时针或逆时针），磁动势的升高和磁动势的变化的代数和为零。假设我们选择顺时针方向，得到：

[ \mathcal{F}_1 - \Phi \mathcal{R}_1 - \Phi \mathcal{R}_2 - \mathcal{F}_2 = 0 ]

其中 ( \Phi ) 是通过电阻的磁通量，( \mathcal{R}_1 ) 和 ( \mathcal{R}_2 ) 是磁阻。如果已知磁动势源和磁阻，可以通过上述公式计算磁通量或其他参数的值。

在电机控制中，尤其是在矢量控制（Field-Oriented Control, FOC）和直接转矩控制（Direct Torque Control, DTC）中，$d$-$q$ 轴是一种常用的数学工具，用于将电机的三相交流量转换为直流量，方便控制。具体来说，$d$ 轴和 $q$ 轴是一个旋转坐标系的两条正交轴，用来表示电机内部的电流、磁链等物理量。这个旋转坐标系与电机的转子磁场保持同步旋转。

DQ轴系

$d$ 轴（直轴）direct axis

• 定义: $d$ 轴是沿着电机转子磁链方向的轴，也就是与转子磁场对齐的方向。平行于磁感线
• 物理意义: 在同步电机中，$d$ 轴电流 ($i_d$) 主要与转子的磁通有关。通过调节 $i_d$，可以控制磁链的大小。在永磁同步电机 (PMSM) 中，通常将 $i_d$ 控制为零，以使得所有电流都用于产生转矩（$q$ 轴上）。
• 作用: 通过控制 $i_d$，可以进行弱磁控制（Field Weakening），以增加电机的最高转速。

$q$ 轴（交轴）quadrature axis

• 定义: $q$ 轴是与 $d$ 轴垂直的轴，位于旋转坐标系中。垂直于磁感线
• 物理意义: $q$ 轴电流 ($i_q$) 主要负责产生电磁转矩。对于永磁同步电机，电磁转矩通常与 $q$ 轴电流成正比。因此，控制 $i_q$ 就可以直接控制电机的转矩输出。
• 作用: 在矢量控制中，通过精确控制 $i_q$，可以实现定转矩控制。

坐标变换

为了实现矢量控制，将电机的三相电流（$i_a$, $i_b$, $i_c$）通过 Clarke 和 Park 变换，转换到 $d$-$q$ 坐标系中。这种变换将原本复杂的三相交流电流转化为两个直流分量 $i_d$ 和 $i_q$，使得电机控制问题变得更为简单和直观。

旋转坐标系（$d$-$q$ 轴）与静止坐标系（$\alpha$-$\beta$ 轴）

• $d$-$q$ 轴: 旋转坐标系，随着电机的转子磁场同步旋转。$d$ 轴与转子磁链对齐，$q$ 轴与 $d$ 轴垂直。
• $\alpha$-$\beta$ 轴: 静止坐标系，不随电机的转子运动。用于将三相电流转化为两相电流，再进一步通过 Park 变换转化为 $d$-$q$ 轴。

总结

• $d$ 轴: 对应于电机转子磁链的方向，控制磁链或磁通。
• $q$ 轴: 与 $d$ 轴垂直，对应于产生转矩的方向，控制电磁转矩。

理解 $d$-$q$ 轴的定义和作用是掌握电机矢量控制的关键，有助于实现高效的电机控制策略，如定转矩控制、弱磁控制等。

⭐为什么不直接从啊abc三项直接变换到dq，还要经过$\alpha-\beta$轴？

1. 简化坐标变换

直接从 $abc$ 坐标系转换到 $d$-$q$ 坐标系是可以的，但这个转换过程将涉及到更复杂的三维空间旋转变换，而通过 $\alpha$-$\beta$ 坐标系可以分解成两个更简单的步骤：

• Clarke 变换（$abc \rightarrow \alpha\beta$）：将三相静止坐标系 ($abc$) 转换为两相静止坐标系 ($\alpha\beta$)。这个变换将三相不对称的信号简化为两相对称的信号。
• Park 变换（$\alpha\beta \rightarrow dq$）：将两相静止坐标系 ($\alpha\beta$) 转换为两相旋转坐标系 ($dq$)。这个变换进一步简化，将电机电流或电压表示为直流量，便于控制。

通过分解这些步骤，变换过程变得更加直观和容易计算。

2. 几何解释

从几何角度来看，$abc$ 三相系统形成一个三维空间，而 $\alpha\beta$ 系统是一个二维平面，进一步将 $\alpha\beta$ 平面旋转就得到 $dq$ 旋转坐标系。这样分步处理简化了数学描述：

• Clarke 变换：投影，将三相系统中的物理量投影到一个二维平面上（$\alpha\beta$ 系统），减少一个维度。
• Park 变换：旋转，将二维平面中的物理量进一步旋转到与电机转子磁场同步的 $dq$ 系统。

这相当于将复杂的三维空间变换拆解为两步操作，分别在二维平面内完成投影和旋转。

3. 数学计算的简化

逐步进行 Clarke 变换和 Park 变换，避免了直接进行三相到旋转坐标系的复杂非线性变换。特别是：

• Clarke 变换：只涉及加权求和，简单且计算量小。
• Park 变换：只是对二维矢量进行旋转，计算上相对简单，且可以直接使用 $sin$ 和 $cos$ 函数。

这种分步变换使得计算更加高效，尤其在嵌入式控制系统中，减少了计算量和实现复杂度。

电机分类

在汽车电子中，常用的电机种类繁多，根据不同的功能和应用场景选择不同类型的电机。以下是一些常见的汽车电子电机类型及其应用：

直流电机（DC Motor）

• 有刷直流电机（Brushed DC Motor）

  • 结构：由定子（永磁体或电磁体）、转子（电枢绕组）和换向器及电刷组成。
  • 工作原理：电流通过电刷和换向器进入转子绕组，产生电磁场。定子和转子的磁场相互作用，产生转矩驱动转子旋转。电刷和换向器的作用是不断切换电流方向，以保持转子连续旋转。
  • 应用：车窗升降、座椅调节、后视镜调整、雨刮器等。
  • **特点：**结构简单、成本低、控制方便。电刷和换向器磨损快，需定期维护；噪音较大；效率较低。
  

• 无刷直流电机（Brushless DC Motor，BLDC）

  • 结构：由定子绕组和转子永磁体组成，没有电刷和换向器，使用电子控制器进行换向。
  • 工作原理：电子控制器根据转子的角度，通过霍尔传感器或无传感器技术控制定子绕组电流，实现电流的换向，产生旋转磁场，驱动转子旋转。
  • 应用：风扇、电动助力转向（EPS）、电动燃油泵、电动水泵、电动空调压缩机等。
  • 特点：效率高、寿命长、维护少，适用于需要高性能和高可靠性的应用。
  

交流电机（AC Motor）

• 异步电动机（Induction Motor）

  • 结构：由定子绕组和转子（通常是鼠笼式转子或绕线转子）组成。
  • 工作原理：定子绕组通入交流电，产生旋转磁场，感应出转子电流。转子电流与定子磁场相互作用，产生转矩驱动转子旋转。转子的转速低于同步转速，形成转差率。
  • 应用：某些混合动力和电动汽车的驱动电机。
  • 特点：结构坚固、成本较低、维护简单，但效率相对较低。

• 同步电动机（Synchronous Motor）

  • 结构：由定子绕组和转子（永磁体或励磁绕组）组成。
  • 工作原理：定子绕组通入交流电，产生旋转磁场。转子上的永磁体或励磁绕组在旋转磁场的作用下，以同步转速旋转，即转子转速与定子磁场的转速相同。
  • 永磁同步电机（Permanent Magnet Synchronous Motor，PMSM）
    • 应用：电动汽车和混合动力汽车的主驱动电机。
    • 特点：效率高、功率密度大、动态响应好，但成本较高。

步进电机（Stepper Motor）

• 结构：由定子绕组和多极转子组成。
• 工作原理：通过控制电流顺序通入定子绕组，产生按步进角移动的旋转磁场，驱动转子逐步旋转，实现精确的位置控制。
• 应用：仪表盘指针驱动、电子节气门控制、HVAC（暖通空调）系统中的风门控制等。
• 特点：能够实现精确的位置控制，适用于需要精确定位的应用。

其他类型电机

• 传动系统中的电机

  • 应用：自动变速器中的电机用于换挡执行、离合器控制等。
  • 特点：需要高精度、高可靠性和快速响应。

• 电机集成模块

  • 应用：集成电机和电子控制单元（ECU）的模块，用于各种车载系统，如电动燃油泵模块、电动水泵模块等。
  • 特点：集成化设计，提高了系统的紧凑性和可靠性。

常见应用场景的电机

1. 动力系统

   • 主驱动电机（电动汽车和混合动力汽车）
   • 电动助力转向（EPS）电机
   • 电动增压器电机

2. 车身控制系统

   • 车窗升降电机
   • 座椅调节电机
   • 后视镜调整电机
   • 雨刮器电机

3. 舒适性和便利性系统

   • 空调系统中的电机（如电动压缩机）
   • 电动尾门电机
   • 电动天窗电机

4. 辅助系统

   • 电动燃油泵电机
   • 电动水泵电机
   • HVAC系统中的风门控制电机

汽车电子中使用的电机种类繁多，不同类型的电机在不同的应用场景中发挥各自的优势。选择合适的电机类型和控制方式，对于提高汽车系统的性能、效率和可靠性至关重要。

常用名词的含义

基波（Fundamental Wave）与驻波（Standing wave）

基波和驻波是波动和信号处理中的两个不同概念，理解它们对于电机、信号处理和物理系统的分析非常重要。以下是对这两个概念的详细解释：

基波

基波（fundamental wave）是指在周期信号或波形中，具有最低频率的正弦波成分。基波决定了信号的基本周期和主要特性。其他频率成分（谐波）是基波频率的整数倍。

特点：

1. 最低频率：基波的频率是周期信号的基本频率，所有谐波的频率都是它的整数倍。
2. 主要能量成分：在许多信号中，基波往往包含了主要的能量成分，是信号的主要部分。
3. 傅里叶分析：通过傅里叶分析，可以将一个复杂的周期信号分解为基波和谐波。

示例：

如果一个信号的基波频率是50 Hz，那么它的谐波频率可能是100 Hz（2倍基波）、150 Hz（3倍基波）等。

驻波

驻波（standing wave）是由两列频率相同、振幅相等、传播方向相反的波相遇并叠加而成的波动形式。驻波具有固定的波节和波腹，波节是振动幅度为零的位置，而波腹是振动幅度最大的位置。

特点：

1. 固定节点：驻波的节点（振动为零的位置）是固定的，不随时间变化。
2. 固定腹部：驻波的腹部（振动最大的位置）也是固定的，不随时间变化。
3. 干涉现象：驻波是两列反向行进波的干涉结果。

示例：

在绳子上来回反射的波，如果绳子的两端固定并产生反射，反射波和入射波相遇就会形成驻波。

比较

特性	基波	驻波
定义	最低频率的正弦波成分	由两列频率相同、振幅相等、传播方向相反的波相遇叠加而成
频率特性	信号的基本频率	固定节点和腹部，不传输能量
应用领域	信号处理、谐波分析、电机驱动	声学、振动分析、机械系统
主要特征	定义信号的基本周期和主要特性	固定的波节点和波腹

基波和驻波在实际应用中的意义

基波在电机和信号处理中的应用

1. 电机驱动：基波用于描述电机的主要驱动频率，优化电机性能。
2. 信号处理：通过分析信号的基波，可以理解信号的主要成分和周期特性，应用于滤波和调制等过程。

驻波在物理系统中的应用

1. 声学：在管乐器和声学系统中，驻波分析用于设计和优化声学特性。
2. 机械振动：在机械系统中，驻波用于分析和控制振动模式，以避免共振和结构损坏。

反电动势（Back EMF）

反电动势是电机在运转过程中产生的电动势，其方向与电源电压相反。它与电机的转速成正比，是无刷直流电机和步进电机控制的重要参数。

霍尔传感器（Hall Sensor）

霍尔传感器是一种用于检测磁场和转子位置的传感器，广泛应用于无刷直流电机（BLDC）和步进电机中，帮助实现精确的位置和速度控制。

矢量控制（Vector Control）

矢量控制是一种高级电机控制方法，通过控制电流矢量来控制电机的转矩和速度，通常用于交流异步电机（感应电机）和同步电机。

转子磁链（Rotor Flux Linkage）

转子磁链是指转子内部磁场与转子绕组的相互作用，影响电机的电磁转矩和性能，是矢量控制中的关键参数。

铁损（Iron Losses）

铁损是指电机铁芯中的能量损耗，包括磁滞损耗和涡流损耗。它们是由于铁芯在交变磁场中磁化和感应电流引起的，影响电机的效率和发热。

锁相环（Phase-Locked Loop, PLL）

锁相环是一种用于同步信号频率和相位的反馈控制系统，常用于电机驱动和通信系统中，以实现精确的速度和位置控制。

齿槽效应（Cogging Torque）

齿槽效应是由于电机定子齿槽与转子磁极相互作用引起的转矩波动，会导致电机运行不平稳，特别是在低速时明显。

谐波失真（Harmonic Distortion）

谐波失真是指由于电流和电压中存在高次谐波分量而引起的波形失真，会影响电机的性能和效率，增加电磁干扰。

额定转矩（Rated Torque）

额定转矩是指电机在额定电压和额定电流下能够持续输出的最大转矩，是电机性能的重要参数。

滑差（Slip）

滑差是指同步电机或感应电机的转子转速与同步转速之间的差异，用于描述转子相对于同步磁场的相对速度。滑差是感应电机产生转矩的关键因素。

饱和效应（Saturation Effect）

饱和效应是指电机铁芯中的磁通密度达到一定程度后，不再线性增加，导致电机的磁化特性非线性。饱和效应会影响电机的性能和控制精度。

无刷直流电机（Brushless DC Motor, BLDC）

无刷直流电机是一种通过电子换向代替机械换向的直流电机，具有高效率、低维护等优点，广泛应用于电动车、无人机等领域。

额定功率（Rated Power）

额定功率是电机在额定电压、额定电流和额定转速下能够持续输出的最大功率，是电机的重要性能指标。

磁阻电机（Reluctance Motor）

磁阻电机是一种利用磁阻原理产生转矩的电机，通过转子和定子间的磁阻差异实现运动，具有简单结构和高效率的特点。

分数槽绕组（Fractional Slot Winding）

分数槽绕组是指每极每相的槽数为分数的绕组方式，可以减少齿槽效应和谐波失真，提高电机的平稳性和效率。

强拉（Pull-in）

强拉指的是电机在较低的速度下，能够成功启动并且将负载带动起来的过程。具体来说，它指电机在施加某个初始电压或电流时，能够克服负载的静摩擦力和惯性，并且迅速达到一个稳定转速的过程。

强拖（Pull-out）

强拖指的是电机在运行过程中，由于负载过大或者突然变化，导致电机无法维持其原本的转速，从而失去同步或者停止转动的现象。简单来说，就是电机在运转时由于负载增加而被“拖”慢甚至停下来的情况。