Bresenham算法
前言
在一个迭代算法中,如果每一步的x,y值都是用前一步的值加上一个增量来获得的,那么就称这种算法为增量算法。Bresenham算法就是一个经典的增量算法,利用前一个像素的信息来计算当前像素的位置,这里所用到的,是中点Bresenham算法。
原理
简单的原理
每一次在主位移方向上走一步,另一个方向上走不走取决于中点误差项的值。给定一条理想直线起点坐标为$P_0(x_0,y_0)$,终点坐标为$p_1(x_1,y_1)$,则可求出直线的隐函数方程: $F(x,y)=y-kx-b=0$。可以得到以下信息

显然可得,对于直线上的点,$F(x,y)=0$;对于直线下方的点,$F(x,y)<0$;对于直线上方的点,$F(x,y)>0$。设直线的斜率为$0≤k≤1$,则$△x≥△y$,所以确定x方向为主位移方向。按照Bresenham原理,x方向上每次加1,y方向上加不加1取决于中点误差项的值。
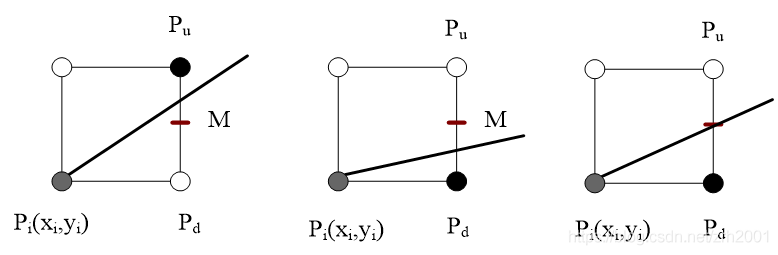
也就是说,当直线准备向主位移x方向走一步时,对于下一步的两点的中点来说,如果该点在直线下方,则选下方的点,反之亦然。
由上述可得,将下一点的中点代入直线隐函数,即得到中点误差项
??=?(??+1,??+0.5)=??+0.5−?(??+1)−?
则易知,di>0,下一个点在直线上方,若di<0,下一个点在直线下方
详细的推导
设线段端点:$(x_1,y_1)$,$(x_2,y_2)$,$∆x$和$∆y$为水平和垂直偏移量,$m$为斜率
$m=\frac{y_2-y_1}{x_2-x_1}=\frac{\Delta y}{\Delta x}$
当$|m| <= 1$时,对于给定的$x$增量$∆x$
$\left{\begin{matrix} \Delta y=m \Delta x \ \Delta x =x_2-x_1.\end{matrix}\right.$
当|m| >= 1时,对于给定的y增量∆y,
$\left{\begin{matrix} \Delta x = \Delta y / m\ \Delta y=y_2-y_1 \end{matrix}\right.$
(当 $0<m < 1$)假设已经确定了要显示的像素$P_k(x_k , y_k)$,那么,需要确定下一点$P_{k+1}$是绘制在$(x_k+1,y_k)$,还是$(x_k+1,y_k+1)$。
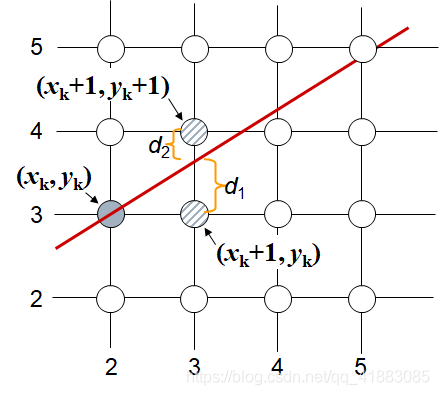
根据直线的方程,直线上$x_k+1$处的y坐标为:
$f(x) = m (x_k + 1) + b$
$d_1=f(x_k+1)-y_k=m(x_k+1)+b -y_k$
$d_2 = (y_k+1) - f(x_k+1) = y_k+1 - m(x_k + 1) - b$
$d_1 - d_2 = 2m (x_k + 1) - 2y_k + 2b$
将$m$带入$d_1 – d_2$中,并变换得:
$p_k = \Delta x (d_1 - d_2) = 2x_k\Delta y - 2y_k\Delta x + c$
其中,$p_k$为算法中**第k*步的决策参数**,c为一常量,其值为$2\Delta y + \Delta x (2b - 1)$,那么:
若$p_k< 0$,即$d_1 < d_2$,有 $y_{k+1} = y_k$
若$p_k\geq 0$, *即$d_1 \geq d_2$,有$y_{k+1} = y_k + 1$
同理,可求得第*k+*1步的决策参数$p_{k+1}$
$p_{k+1} = 2x_{k+1} \Delta y +1 - 2y_{k+1}\Delta x + c$
因此,有如下递推关系:
$p_{k+1}- p_k = (x_{k+1} - x_k)2\Delta y - (y_{k+1} - y_k) 2\Delta x$
因为$0<m<1$ 因此
$x_{k+1} = x_k + 1$,带入上式得:
$p_{k+1} - p_k = 2\Delta y - 2(y_{k+1} - y_k)\Delta x$
其中,$y_{k+1} - y_k$的值取决于$p_k$的值:
当$p_k < 0$时,$y_{k+1} = y_k$,$p_{k+1} = p_k + 2\Delta y$
当$p_k \geq 0$时,$y_{k+1} = y_{k} + 1$,$p_{k+1} = p_k + 2\Delta y - 2\Delta x$
Bresenham算法描述 (0 < *m* < 1)
算法从线段的起始端点开始,反复计算每个点的决策参数并绘制像素。
起始端点$(x_0 , y_0)$处的决策参数$p_0$为:
$d_1 = y - y_0 = m (x_0 + 1) + b - y_0 = m$
$d_2 = (y_0+1) - y = y_0+1 - m (x_0 + 1) - b = 1 - m$
$d_1 - d_2 = 2m - 1$
$p_0 = (d_1 - d_2)\Delta x = (2m - 1)\Delta x = 2\Delta y - \Delta x$
算法:
1、输入线段的两个端点,并将左端点存储在(x
$(x_0 , y_0)$中;
2、将$(x_0 , y_0)$装入帧缓冲器,画出第一个点;
3、计算常量∆x,∆y,2∆y 和2∆y – 2∆x,并得到决策参数的第一个值:$p_0= 2\Delta y - \Delta x$
4、从$k= 0$开始,在沿线的每个$x_k$处,进行下列检测:
若$p_k < 0$,下一个待画点是$(x_k+1, y_k )$,且$p_{k+1} = p_k + 2\Delta y$
若$p_k\geq 0$,下一个待画点是$(x_k+1, y_k+1)$,且$p_{k+1} = p_k+ 2\Delta y -2\Delta x$
5、重复步骤4,共∆x次。
基本步骤
Bresenham算法是一种用于计算直线在离散坐标系统中的像素点的算法。它是一种高效的算法,可以在计算机图形学和数字图像处理中广泛应用。
该算法基于直线的斜率进行计算,从直线的起点到终点逐步确定像素点的位置。Bresenham算法的主要思想是通过利用整数运算来逐步逼近直线的路径,避免了使用浮点数运算,从而提高了计算效率。
以下是Bresenham算法的基本步骤:
-
根据起点和终点的坐标确定直线的斜率。如果斜率绝对值大于1,则将坐标系进行旋转,将斜率绝对值控制在[0, 1]范围内。
-
初始化直线起点的坐标(x0, y0)和终点的坐标(x1, y1)。
-
计算直线在x轴上的增量(dx = |x1 - x0|)和在y轴上的增量(dy = |y1 - y0|)。
-
初始化误差项(error = dx / 2)和步长(ystep = 1 if y0 < y1 else -1)。
-
从起点开始,逐步计算每个像素点的位置,并绘制。
-
在每一步中,根据误差项的值判断是沿着x轴方向移动还是沿着y轴方向移动。如果误差项大于等于0.5,则说明应该向y轴方向移动一步,并更新误差项(error = error - 1);否则只需更新误差项(error = error)。
-
在x轴上每一步移动一个像素点,即更新x坐标(x = x + 1)。
-
根据斜率的正负情况,更新y坐标(y = y ± ystep)。
-
重复步骤5至步骤8,直到达到终点。
通过以上步骤,Bresenham算法可以计算出
hector_mapping/include/hector_slam_lib/map/OccGridMapBase.h
//应用bresenham 画线
inline void updateLineBresenhami( const Eigen::Vector2i& beginMap, const Eigen::Vector2i& endMap, unsigned int max_length = UINT_MAX){
int x0 = beginMap[0];
int y0 = beginMap[1];
//check if beam start point is inside map, cancel update if this is not the case
//检查光束起点是否在地图内,如果不是这种情况,请取消更新
if ((x0 < 0) || (x0 >= this->getSizeX()) || (y0 < 0) || (y0 >= this->getSizeY())) {
return;
}
int x1 = endMap[0];
int y1 = endMap[1];
//std::cout << " x: "<< x1 << " y: " << y1 << " length: " << length << " ";
//check if beam end point is inside map, cancel update if this is not the case
//检查光束端点是否在地图内,如果不是这种情况,请取消更新
if ((x1 < 0) || (x1 >= this->getSizeX()) || (y1 < 0) || (y1 >= this->getSizeY())) {
return;
}
int dx = x1 - x0;
int dy = y1 - y0;
unsigned int abs_dx = abs(dx);//dx的绝对值
unsigned int abs_dy = abs(dy);//dy的绝对值
//offset_dx表示在每一步水平方向上的偏移量,offset_dy表示在每一步垂直方向上的偏移量
int offset_dx = util::sign(dx);//根据dx的正负情况,设置x方向的偏移量。如果dx大于0,偏移量为1;如果dx小于0,偏移量为-1;如果dx等于0,偏移量为0
int offset_dy = util::sign(dy) * this->sizeX;//根据dy的正负情况,设置y方向的偏移量。如果dy大于0,偏移量为sizeX;如果dy小于0,偏移量为-sizeX;如果dy等于0,偏移量为0。sizeX表示地图的水平方向上的尺寸。
//计算起点在地图上的偏移量,将起点的y坐标乘以this->sizeX(水平方向尺寸),然后加上起点的x坐标。
unsigned int startOffset = beginMap.y() * this->sizeX + beginMap.x();//感觉是坐标(x,y),也就起始点的坐标
//if x is dominant
//如果 x 占主导地位
if(abs_dx >= abs_dy){
int error_y = abs_dx / 2;
bresenham2D(abs_dx, abs_dy, error_y, offset_dx, offset_dy, startOffset);
}else{
//otherwise y is dominant
//如果 y占主导地位
int error_x = abs_dy / 2;
bresenham2D(abs_dy, abs_dx, error_x, offset_dy, offset_dx, startOffset);
}
unsigned int endOffset = endMap.y() * this->sizeX + endMap.x();
this->bresenhamCellOcc(endOffset);
}
hector_mapping/include/hector_slam_lib/map/OccGridMapBase.h
bresenham2D(abs_dx, abs_dy, error_y, offset_dx, offset_dy, startOffset);
/*unsigned int abs_da 和 unsigned int abs_db:代表直线在两个轴上的绝对增量(分别对应水平和垂直方向)。
int error_b:表示垂直方向的错误项,初始值为偏移量在垂直方向上的增量的一半。
int offset_a 和 int offset_b:分别是水平方向和垂直方向上的偏移量。
unsigned int offset:表示当前绘制的像素在地图上的偏移量。
unsigned int max_length:限定绘制长度的最大值。 */
inline int bresenham2D(unsigned int abs_da, unsigned int abs_db, int error_b, int offset_a, int offset_b,
unsigned int offset, unsigned int max_length){
unsigned int end = std::min(max_length, abs_da);//计算绘制的结束点,取max_length和abs_da的较小值。
const std::vector<int8_t>& data = map_ptr_->data;//获取地图数据的引用,存储在const std::vector<int8_t>& data中,表示地图上的单元格数据
for(unsigned int i = 0; i < end; ++i){
if (data[offset] == 100){//检查当前绘制的像素是否被标记为100
return static_cast<int>(offset);//返回当前像素的偏移量
}
offset += offset_a;//更新当前像素的偏移量,增加偏移量在水平方向上的值(offset_a)。
error_b += abs_db;//更新垂直方向上的错误项(error_b),加上abs_db。
if((unsigned int)error_b >= abs_da){////如果垂直方向上的错误项(error_b)超过了水平方向上的增量(abs_da),则更新当前像素的偏移量,增加偏移量在垂直方向上的值(offset_b),并减去abs_da。
offset += offset_b;
error_b -= abs_da;
}
}
return -1;//循环结束后,如果没有找到被占用的像素,则返回-1
//at(offset);
}
hector_mapping/include/hector_slam_lib/map/OccGridMapBase.h
bresenham2D(abs_dx, abs_dy, error_y, offset_dx, offset_dy, startOffset);
// 进行bresenham画线
inline void bresenham2D( unsigned int abs_da, unsigned int abs_db, int error_b, int offset_a, int offset_b, unsigned int offset){
// 先把起点格子设置成free
this->bresenhamCellFree(offset);
unsigned int end = abs_da-1;
for(unsigned int i = 0; i < end; ++i){
offset += offset_a;
// 对应 Sub += dy/dx, 这里的实现是对 左右两边同乘 dx 后的结果
error_b += abs_db;
// 判断 Sub > 0
if((unsigned int)error_b >= abs_da){
offset += offset_b;
// 对应Sub += dy/dx - 1, dy/dx 在之前加过了,所以这里只减 1 ,再左右两边同乘 dx
error_b -= abs_da;
}
// 再将路径上的其他点设置成free
this->bresenhamCellFree(offset);
}
}
