局部路径规划，常用的算法有栅格法、人工势场法、遗传算法、空间搜索法、层次法、动作行为法、Dijkstra算法、Lee算法、Floyd算法等

人工势场法

人工势场法是机器人路径规划算法中一种简单有效的方法。人工势场法的基本思想是在移动机器人的工作环境中构造一个人工势场，势场中包括斥力极和吸引极,不希望机器人进入的区域和障碍物定义为斥力极,目标及建议机器人进入的区域定义为引力极,使得在该势场中的移动机器人受到其目标位姿引力场和障碍物周围斥力场的共同作用,朝目标前进。 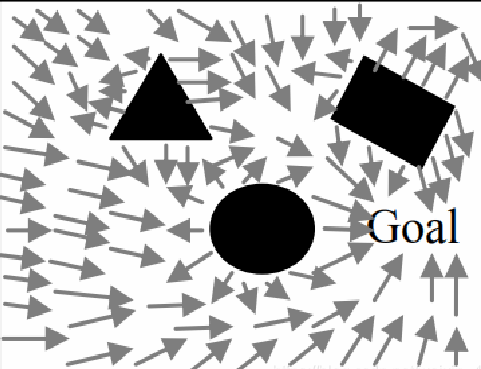概念图如图所示，人工势场就像构建了一个吸铁石，包括引力场和斥力场。黑色为障碍物，箭头为智能体要运动的方向，目标点为“Goal”。智能体按照箭头的方向到达“Goal”，目标点像有着“吸引力”一样吸引着智能体靠近。而在障碍物附近，智能体逆着箭头的方向，好像对智能体产生“排斥力”。智能体前进的方向就是这两种力的合力的方向。

遗传算法

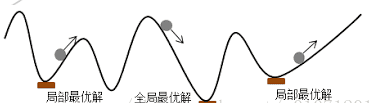
遗传算法（Genetic Algorithm, GA）起源于对生物系统所进行的计算机模拟研究。它是模仿自然界生物进化机制发展起来的随机全局搜索和优化方法，借鉴了达尔文的进化论和孟德尔的遗传学说。其本质是一种高效、并行、全局搜索的方法，能在搜索过程中自动获取和积累有关搜索空间的知识，并自适应地控制搜索过程以求得最佳解。 遗传算法中每一条染色体，对应着遗传算法的一个解决方案，一般我们用适应性函数（fitness function）来衡量这个解决方案的优劣。所以从一个基因组到其解的适应度形成一个映射。可以把遗传算法的过程看作是一个在多元函数里面求最优解的过程。可以这样想象，这个多维曲面里面有数不清的“山峰”，而这些山峰所对应的就是局部最优解。而其中也会有一个“山峰”的海拔最高的，那么这个就是全局最优解。而遗传算法的任务就是尽量爬到最高峰，而不是陷落在一些小山峰。（另外，值得注意的是遗传算法不一定要找“最高的山峰”，如果问题的适应度评价越小越好的话，那么全局最优解就是函数的最小值，对应的，遗传算法所要找的就是“最深的谷底”） 模拟物竞天择的生物进化过程，通过维护一个潜在解的群体执行了多方向的搜索，并支持这些方向上的信息构成和交换。是以面为单位的搜索，比以点为单位的搜索，更能发现全局最优解。（在遗传算法中，有很多袋鼠，它们降落到喜玛拉雅山脉的任意地方。这些袋鼠并不知道它们的任务是寻找珠穆朗玛峰。但每过几年，就在一些海拔高度较低的地方射杀一些袋鼠，并希望存活下来的袋鼠是多产的，在它们所处的地方生儿育女。）（或者换个说法。从前，有一大群袋鼠，它们被莫名其妙的零散地遗弃于喜马拉雅山脉。于是只好在那里艰苦的生活。海拔低的地方弥漫着一种无色无味的毒气，海拔越高毒气越稀薄。可是可怜的袋鼠们对此全然不觉，还是习惯于活蹦乱跳。于是，不断有袋鼠死于海拔较低的地方，而越是在海拔高的袋鼠越是能活得更久，也越有机会生儿育女。就这样经过许多年，这些袋鼠们竟然都不自觉地聚拢到了一个个的山峰上，可是在所有的袋鼠中，只有聚拢到珠穆朗玛峰的袋鼠被带回了美丽的澳洲。）

遗传算法的实现过程

遗传算法的实现过程实际上就像自然界的进化过程那样。首先寻找一种对问题潜在解进行“数字化”编码的方案。（建立表现型和基因型的映射关系）然后用随机数初始化一个种群（那么第一批袋鼠就被随意地分散在山脉上），种群里面的个体就是这些数字化的编码。接下来，通过适当的解码过程之后（得到袋鼠的位置坐标），用适应性函数对每一个基因个体作一次适应度评估（袋鼠爬得越高，越是受我们的喜爱，所以适应度相应越高）。用选择函数按照某种规定择优选择（我们要每隔一段时间，在山上射杀一些所在海拔较低的袋鼠，以保证袋鼠总体数目持平。）。让个体基因变异（让袋鼠随机地跳一跳）。然后产生子代（希望存活下来的袋鼠是多产的，并在那里生儿育女）。遗传算法并不保证你能获得问题的最优解，但是使用遗传算法的最大优点在于你不必去了解和操心如何去“找”最优解。（你不必去指导袋鼠向那边跳，跳多远。）而只要简单的“否定”一些表现不好的个体就行了。（把那些总是爱走下坡路的袋鼠射杀，这就是遗传算法的精粹！）

遗传算法的一般步骤：

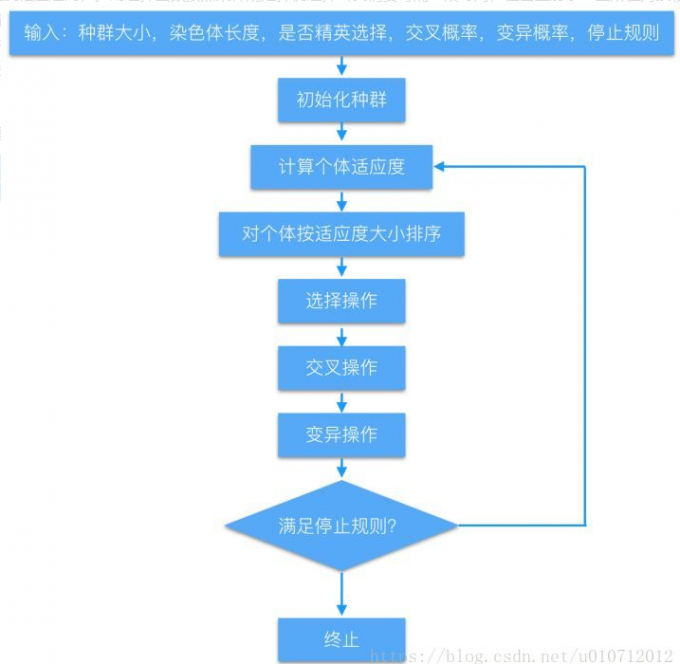1.评估每条染色体所对应个体的适应度。

2.遵照适应度越高，选择概率越大的原则，从种群中选择两个个体作为父方和母方。

3.抽取父母双方的染色体，进行交叉，产生子代。

4.对子代的染色体进行变异。

5.重复2，3，4步骤，直到新种群的产生。

结束循环。

空间搜索法

GeoHash 是一种对地理坐标进行编码的方法，将二维坐标映射为一个字符串。每个字符串代表一个特定的矩形，在该矩形范围内的所有坐标都共用这个字符串。那我们如何划分矩形区间呢？如果以本初子午线、赤道为界，地球可以分成 4 个部分。在垂直方向，如果纬度在 [-90, 0) 区间范围内用二进制 0 代表，即用 0 来表示下面的区间，如果在 (0, 90] 区间内范围用二进制 1 代表，即用 1 表示上面的区间；同样在水平方向，经度在 [-180, 0) 区间范围内用二进制 0 代表，即用 0 来表示左边的区间，如果在 (0, 180] 区间范围内用二进制 1 代表，即用 1 表示右边的区间。那么地球可以分成如下 4 个部分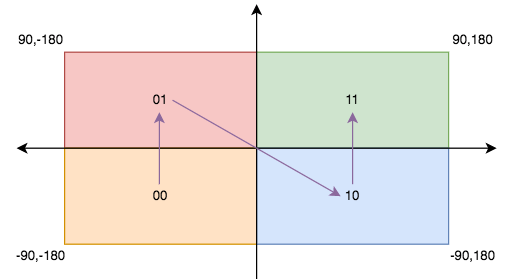： 我们可以继续拆分，将整个地球初始分割成 4*8=32 个网格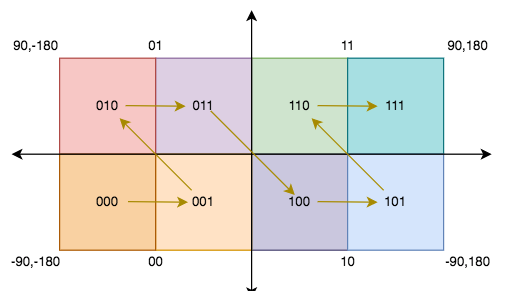： 每个网格使用一个 Base32 的字母编码表示：

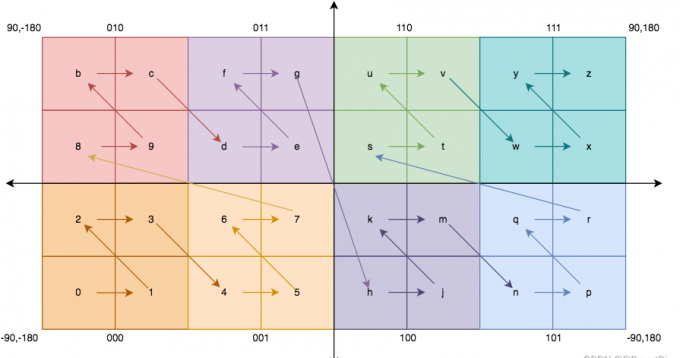
实现原理

对一个地理坐标实现 GeoHash 编码时，需要通过如下步骤实现将一个经纬度坐标转换成一个 GeoHash 编码字符串： 1.指定一个位置的经纬度坐标值，将纬度和经度分别编码为由 0 和 1 组成的二进制数字串 2.按照’偶数位放经度，奇数位放纬度’的原则，将得到的二进制编码穿插组合，得到一个新的二进制串 3.合并后的二进制串，按照从前往后，每隔 5 位，换算成十进制数字，最后不足 5 位的用 0 补齐 4.根据 base32 的对照表，将十进制数字翻译成字符串，即得到地理坐标对应的目标 GeoHash 字符串

Dijkstra算法

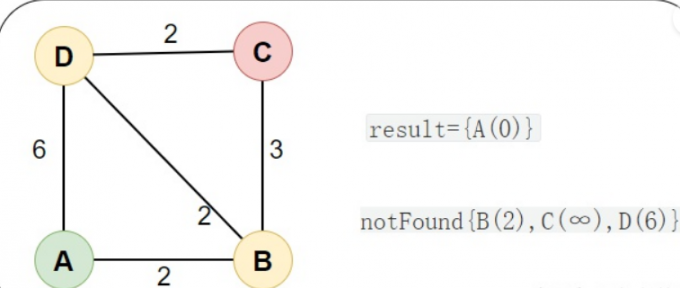
Dijkstra 算法是一个基于「贪心」、「广度优先搜索」、「动态规划」求一个图中一个点到其他所有点的最短路径的算法，时间复杂度 O(n2)。每次从 「未求出最短路径的点」中 取出 距离距离起点 最小路径的点，以这个点为桥梁 刷新「未求出最短路径的点」的距离。 初始，result={A(0)} 中只有起点 A，notFound={B(2),C(∞),D(6)} 中是除了 A 点的其他点，里面的值是到起点的距离（例如 B(2) 代表 B点到起点的距离为 2） 然后，从「未求出最短路径的点」notFound 中取出 最短路径的点 B(2) ，然后通过 B(2) 为桥梁 刷新「未求出最短路径的点」的距离

取出最短路径的点

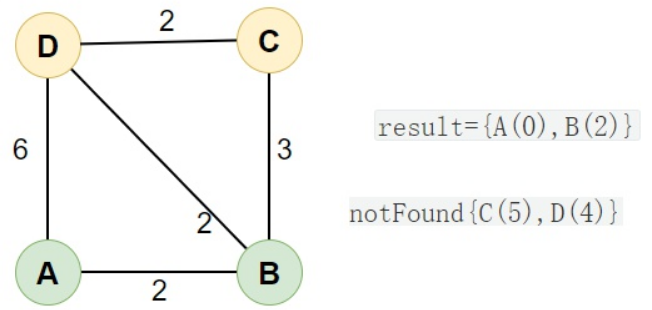
从「未求出最短路径的点」notFound 中取出最短路径的点B(2)，放入结果 result 中，结果如下：「未求出最短路径点」 notFound={C(∞),D(6)}，「已求出最短路径的点 」result={A(0),B(2)}

刷新距离

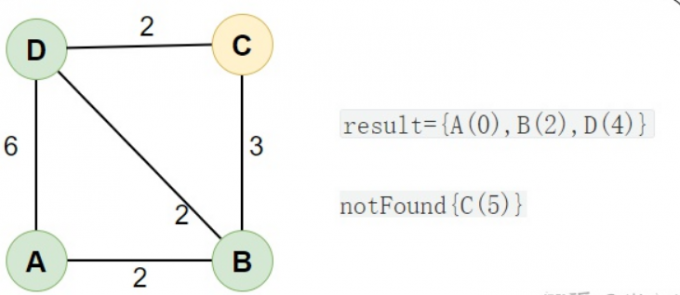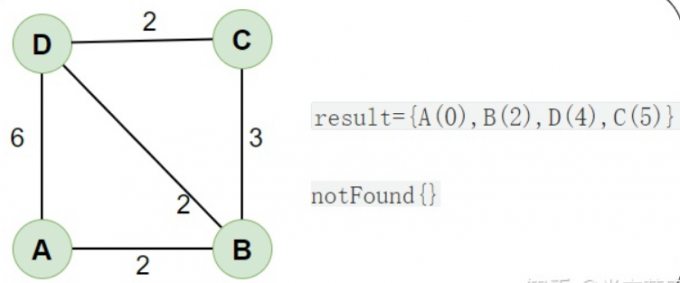
通过 B(2) 为桥梁，刷新距离。 例如 AD = 6 < AB + BD = 4 以 B(2) 为桥梁的距离更短，就刷新「未求出最短路径点」D(6) 的距离为 D(4) notFound={C(∞),D(4)}，同理刷新 C(∞) 的距离为 C(5) ，最后结果如下：「未求出最短路径点」 notFound={C(5),D(4)} ，「已求出最短路径的点**」result={A(0),B(2)}** 然后，从「未求出最短路径的点」notFound 中取出 最短路径的点 D(4) ，然后通过 D(4) 为桥梁 刷新「未求出最短路径的点」的距离。同理，最后结果如下：「未求出最短路径点」 notFound={C(5)} ，「已求出最短路径的点」result={A(0),B(2),D(4)} 然后，从「未求出最短路径的点」notFound 中取出 最短路径的点 C(5) ，算法结束：result={A(0),B(2),D(4),C(5)} 就是最终所求的最短距离 参考： https://blog.csdn.net/SunnyYoona/article/details/125491727 https://blog.csdn.net/u010712012/article/details/82457655 https://zhuanlan.zhihu.com/p/338414118