这是另一个激光slam系统，特点是用IMU解决了激光的运动畸变问题，另外主要贡献还是对扫描匹配和栅格地图的构建提出了新的思路。下面，我将从阅读源码的角度，对该slam系统做一个简单的分析，也当作是个人的学习笔记。
参考：Hector SLAM算法学习与代码解析 HectorSLAM论文解析・代码重写 Hector SLAM论文翻译
一、代码框架
该开源系统的主要代码在hector_mapping文件夹中，文件夹里有src文件夹和include文件夹，包含了算法所有的核心代码。
通过对源码的梳理，整理出了如下流程图：
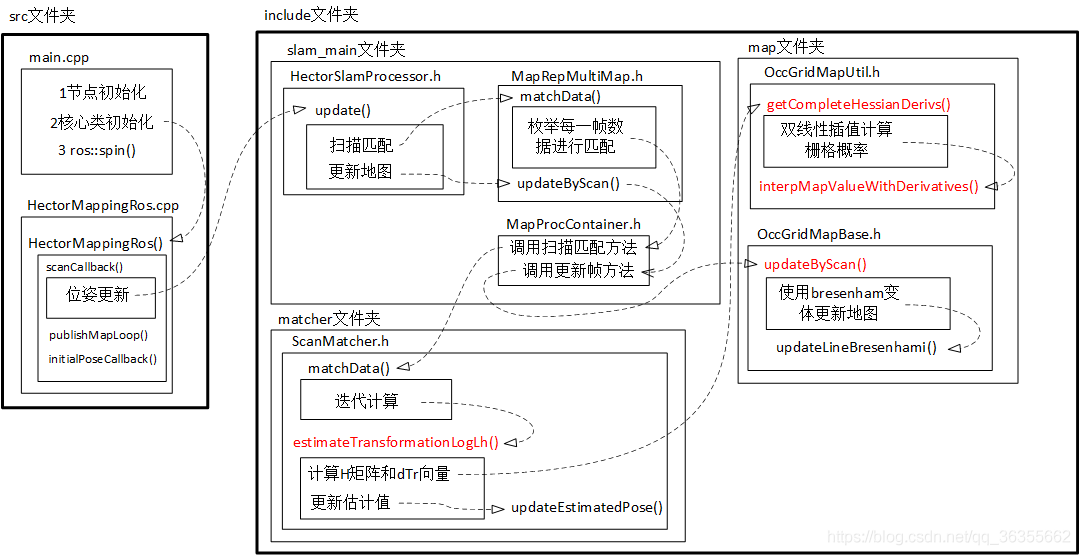同样地，红色标注的函数是需要重点关注的函数。
二、扫描匹配
首先，来了解一下其中的扫描匹配部分，创新点就是使用非线性优化——高斯牛顿法获得最优匹配。
`/**
* @brief 最终的扫描匹配函数
* @param beginEstimateWorld 世界坐标系中估计的初始位姿
* @param gridMapUtil 栅格地图处理的常用方法
* @param dataContainer 激光数据
* @param covMatrix 协方差矩阵
* @param maxIterations 最大迭代次数
**/
Eigen::Vector3f matchData(const Eigen::Vector3f& beginEstimateWorld, ConcreteOccGridMapUtil& gridMapUtil, const DataContainer& dataContainer, Eigen::Matrix3f& covMatrix, int maxIterations)
{
//交互信息显示
if (drawInterface){
drawInterface->setScale(0.05f);
drawInterface->setColor(0.0f,1.0f, 0.0f);
drawInterface->drawArrow(beginEstimateWorld);
Eigen::Vector3f beginEstimateMap(gridMapUtil.getMapCoordsPose(beginEstimateWorld));
drawScan(beginEstimateMap, gridMapUtil, dataContainer);
drawInterface->setColor(1.0,0.0,0.0);
}
if (dataContainer.getSize() != 0) {
Eigen::Vector3f beginEstimateMap(gridMapUtil.getMapCoordsPose(beginEstimateWorld));
Eigen::Vector3f estimate(beginEstimateMap);
//迭代计算，核心函数
estimateTransformationLogLh(estimate, gridMapUtil, dataContainer);
//再次迭代，计算最优解
int numIter = maxIterations;
for (int i = 0; i < numIter; ++i) {
estimateTransformationLogLh(estimate, gridMapUtil, dataContainer);
//交互信息显示
if(drawInterface){
float invNumIterf = 1.0f/static_cast<float> (numIter);
drawInterface->setColor(static_cast<float>(i)*invNumIterf,0.0f, 0.0f);
drawInterface->drawArrow(gridMapUtil.getWorldCoordsPose(estimate));
}
//调试信息显示
if(debugInterface){
debugInterface->addHessianMatrix(H);
}
}
//交互信息显示
if (drawInterface){
drawInterface->setColor(0.0,0.0,1.0);
drawScan(estimate, gridMapUtil, dataContainer);
}
estimate[2] = util::normalize_angle(estimate[2]);
covMatrix = Eigen::Matrix3f::Zero();
covMatrix = H;
return gridMapUtil.getWorldCoordsPose(estimate);
}
return beginEstimateWorld;
}`
其实，函数体中只有一个子函数调用是重点，就是 estimateTransformationLogLh(estimate, gridMapUtil, dataContainer)，下面看看这个函数：
`/**
* @brief 非线性最小二乘计算，该函数在循环内被调用
* @param estimate 世界坐标系中估计的初始位姿
* @param gridMapUtil 栅格地图处理的常用方法
* @param dataPoints 激光数据
**/
bool estimateTransformationLogLh(Eigen::Vector3f& estimate, ConcreteOccGridMapUtil& gridMapUtil, const DataContainer& dataPoints)
{
//核心函数，计算H矩阵和dTr向量
gridMapUtil.getCompleteHessianDerivs(estimate, dataPoints, H, dTr);
//判断增量非0,避免无用计算
if ((H(0, 0) != 0.0f) && (H(1, 1) != 0.0f)) {
Eigen::Vector3f searchDir (H.inverse() * dTr);//计算迭代增量
//对增量进行限位处理
if (searchDir[2] > 0.2f) {
searchDir[2] = 0.2f;
std::cout << "SearchDir angle change too large\n";
} else if (searchDir[2] < -0.2f) {
searchDir[2] = -0.2f;
std::cout << "SearchDir angle change too large\n";
}
//更新估计值 estimate += searchDir
updateEstimatedPose(estimate, searchDir);
return true;
}
return false;
}`
同样的，里面仍然是只有一个函数调用是重点，就是gridMapUtil.getCompleteHessianDerivs(estimate, dataPoints, H, dTr)，我们找到这个函数如下：
`/**
* @brief 计算矩阵H和向量dTr
* @param pose 世界坐标系中估计的机器人的初始位姿
* @param dataPoints 激光数据
* @param H hessian矩阵
* @param dTr 增量
**/
void getCompleteHessianDerivs(const Eigen::Vector3f& pose, const DataContainer& dataPoints, Eigen::Matrix3f& H, Eigen::Vector3f& dTr)
{
int size = dataPoints.getSize();
//由位姿算出转换二维转换矩阵
Eigen::Affine2f transform(getTransformForState(pose));
float sinRot = sin(pose[2]);
float cosRot = cos(pose[2]);
H = Eigen::Matrix3f::Zero();
dTr = Eigen::Vector3f::Zero();
//对一帧激光中的每个数据点进行处理
for (int i = 0; i < size; ++i) {
const Eigen::Vector2f& currPoint (dataPoints.getVecEntry(i));//从scan中取出每一个点
//通过双线性插值计算栅格概率
Eigen::Vector3f transformedPointData(interpMapValueWithDerivatives(transform * currPoint));
//击中点的栅格概率值应该是1,计算匹配误差(1-M(Pm))
float funVal = 1.0f - transformedPointData[0];
//更新位移增量
dTr[0] += transformedPointData[1] * funVal;
dTr[1] += transformedPointData[2] * funVal;
// | -sin -cos 0 | | Xr | | Xdec |
// ( | cos -sin 0 | * | Yr | ).tanspose() * | Ydec |
// | 0 0 1 | | Rr | | ---- |
//计算旋转误差(由map->base_link)
float rotDeriv = ((-sinRot * currPoint.x() - cosRot * currPoint.y()) * transformedPointData[1] +
(cosRot * currPoint.x() - sinRot * currPoint.y()) * transformedPointData[2]);
//更新角度增量
dTr[2] += rotDeriv * funVal;
//更新海塞矩阵
H(0, 0) += util::sqr(transformedPointData[1]);
H(1, 1) += util::sqr(transformedPointData[2]);
H(2, 2) += util::sqr(rotDeriv);
H(0, 1) += transformedPointData[1] * transformedPointData[2];
H(0, 2) += transformedPointData[1] * rotDeriv;
H(1, 2) += transformedPointData[2] * rotDeriv;
}
H(1, 0) = H(0, 1);
H(2, 0) = H(0, 2);
H(2, 1) = H(1, 2);
}`
该函数用到了双线性插值，就是论文中主要讲述的部分： Eigen::Vector3f transformedPointData(interpMapValueWithDerivatives(transform * currPoint)); 下面再看看这个函数，对照论文公式你会发现非常容易理解（除了一些小问题）：
`/**
* @brief 地图双线性插值
* @param coords 栅格坐标
* @return 返回三维向量，三个值包含栅格坐标对应的概率值，对y的偏导值，对x的偏导值
**/
Eigen::Vector3f interpMapValueWithDerivatives(const Eigen::Vector2f& coords)
{
//检查coords坐标是否是在地图坐标范围内
if (concreteGridMap->pointOutOfMapBounds(coords)){
return Eigen::Vector3f(0.0f, 0.0f, 0.0f);
}
//对坐标进行向下取整，即得到坐标(x0,y0)
Eigen::Vector2i indMin(coords.cast<int>());
//得到双线性插值的因子
// | x | | x0 | | x-x0 |
// | | - | | = | |
// | y | | y0 | | y-y0 |
Eigen::Vector2f factors(coords - indMin.cast<float>());
int sizeX = concreteGridMap->getSizeX();//获得地图的X方向最大边界
int index = indMin[1] * sizeX + indMin[0];//将地图坐标转换成地图数组索引
// 获取当前坐标周围的4个网格点的网格值。 首先检查缓存数据，如果没有包含过滤器gridPoint with gaussian并存储在缓存中。
if (!cacheMethod.containsCachedData(index, intensities[0])) {
intensities[0] = getUnfilteredGridPoint(index);//得到M(P00),P00(x0,y0)
cacheMethod.cacheData(index, intensities[0]);
}
++index;
if (!cacheMethod.containsCachedData(index, intensities[1])) {
intensities[1] = getUnfilteredGridPoint(index);//得到M(P10),P10(x0,y1)
cacheMethod.cacheData(index, intensities[1]);
}
index += sizeX-1;
if (!cacheMethod.containsCachedData(index, intensities[2])) {
intensities[2] = getUnfilteredGridPoint(index);//得到M(P01),P10(x1,y0)
cacheMethod.cacheData(index, intensities[2]);
}
++index;
if (!cacheMethod.containsCachedData(index, intensities[3])) {
intensities[3] = getUnfilteredGridPoint(index);//得到M(P11),P10(x1,y1)
cacheMethod.cacheData(index, intensities[3]);
}
float dx1 = intensities[0] - intensities[1];//求得(M(P00) - M(P10))的值
float dx2 = intensities[2] - intensities[3];//求得(M(P01) - M(P11))的值
float dy1 = intensities[0] - intensities[2];//求得(M(P00) - M(P01))的值
float dy2 = intensities[1] - intensities[3];//求得(M(P10) - M(P11))的值
//得到双线性插值的因子,注意x0+1=x1,y0+1=y1,则
// | x-x0 | | 1-x+x0 | | x1-x |
// 1 - | | = | | = | |
// | y-y0 | | 1-y+y0 | | y1-x |
float xFacInv = (1.0f - factors[0]);//求得(x1-x)的值
float yFacInv = (1.0f - factors[1]);//求得(y1-y)的值
// y-y0 | x-x0 x1-x | y1-y | x-x0 x1-x |
//M(Pm) = ------|------ M(P11) + ------ M(P01)| + ------|------ M(P10) + ------ M(P00)|
// y1-y0| x1-x0 x1-x0 | y1-y0| x1-x0 x1-x0 |
//注意：此处y1-y0=x1-x0=1,那么对应函数返回值，可以写成
//M(Pm) = (M(P00) * (x1-x) + M(P10) * (x-x0)) * (y1-y) + (M(P01) * (x1-x) + M(P11) * (x-x0)) * (y-y0)
// d(M(Pm)) y-y0 | | y1-y | |
//---------- = ------| M(P11) - M(P01)| + ------| M(P10) - M(P00)|
// dx y1-y0| | y1-y0| |
//同理，化简可得 d(M(Pm))/dx = -((M(P00) - M(P10)) * (y1-y) + (M(P01) - M(P11)) * (y-y0))
//同样地，也有 d(M(Pm))/dy = -((M(P00) - M(P01)) * (x1-x) + (M(P10) - M(P11)) * (x-x0))
return Eigen::Vector3f(
((intensities[0] * xFacInv + intensities[1] * factors[0]) * (yFacInv)) +
((intensities[2] * xFacInv + intensities[3] * factors[0]) * (factors[1])),
-((dx1 * xFacInv) + (dx2 * factors[0])),
-((dy1 * yFacInv) + (dy2 * factors[1]))
);
}`
仔细对比公式，会发现代码和公式对不上的，这其实是源码的一个bug（github有人提问），实际使用时影响并不大。因为两个方向上栅格梯度相近，所以不会有很大的影响。
三、地图构建
该系统本质上就是构建了一个多分辨率的地图，默认是三层，在每一层上进行的操作类似。
`MapRepMultiMap(float mapResolution, int mapSizeX, int mapSizeY, unsigned int numDepth, const Eigen::Vector2f& startCoords, DrawInterface* drawInterfaceIn, HectorDebugInfoInterface* debugInterfaceIn)
{
//unsigned int numDepth = 3;
Eigen::Vector2i resolution(mapSizeX, mapSizeY);
float totalMapSizeX = mapResolution * static_cast<float>(mapSizeX);
float mid_offset_x = totalMapSizeX * startCoords.x();
float totalMapSizeY = mapResolution * static_cast<float>(mapSizeY);
float mid_offset_y = totalMapSizeY * startCoords.y();
for (unsigned int i = 0; i < numDepth; ++i){
std::cout << "HectorSM map lvl " << i << ": cellLength: " << mapResolution << " res x:" << resolution.x() << " res y: " << resolution.y() << "\n";
GridMap* gridMap = new hectorslam::GridMap(mapResolution,resolution, Eigen::Vector2f(mid_offset_x, mid_offset_y));
OccGridMapUtilConfig<GridMap>* gridMapUtil = new OccGridMapUtilConfig<GridMap>(gridMap);
ScanMatcher<OccGridMapUtilConfig<GridMap> >* scanMatcher = new hectorslam::ScanMatcher<OccGridMapUtilConfig<GridMap> >(drawInterfaceIn, debugInterfaceIn);
mapContainer.push_back(MapProcContainer(gridMap, gridMapUtil, scanMatcher));
resolution /= 2;
mapResolution*=2.0f;
}
dataContainers.resize(numDepth-1);
}`
然后，对每一帧数据进行地图更新，利用bresenham划线算法计算激光途经栅格。
`/**
* @brief 使用给定的扫描数据和机器人姿势更新地图。
* @param dataContainer 激光数据
* @param robotPoseWorld 机器人在世界坐标系下的2D位姿
*/
void updateByScan(const DataContainer& dataContainer, const Eigen::Vector3f& robotPoseWorld)
{
currMarkFreeIndex = currUpdateIndex + 1;
currMarkOccIndex = currUpdateIndex + 2;
//将世界坐标中的位姿转换为地图坐标中的位姿。
Eigen::Vector3f mapPose(this->getMapCoordsPose(robotPoseWorld));
//获得2D均匀变换，可以左对乘机器人坐标向量，以获得该向量的世界坐标。
Eigen::Affine2f poseTransform((Eigen::Translation2f(
mapPose[0], mapPose[1]) * Eigen::Rotation2Df(mapPose[2])));
//获取地图坐标中所有激光束的起点（对于所有激光束相同，存储在dataContainer中的机器人坐标中）。
Eigen::Vector2f scanBeginMapf(poseTransform * dataContainer.getOrigo());
//获取激光束起始点的整数向量。（向上取整）
Eigen::Vector2i scanBeginMapi(scanBeginMapf[0] + 0.5f, scanBeginMapf[1] + 0.5f);
//获取当前扫描中的有效光束数。
int numValidElems = dataContainer.getSize();
//std::cout << "\n maxD: " << maxDist << " num: " << numValidElems << "\n";
//迭代计算所有有效激光束
for (int i = 0; i < numValidElems; ++i) {
//得到当前激光束末端点的地图坐标
Eigen::Vector2f scanEndMapf(poseTransform * (dataContainer.getVecEntry(i)));
//std::cout << "\ns\n" << scanEndMapf << "\n";
//进行向上取整操作
scanEndMapf.array() += (0.5f);
//得到当前激光束末端点的整数地图坐标
Eigen::Vector2i scanEndMapi(scanEndMapf.cast<int>());
//使用bresenham变体更新地图，以在地图坐标中绘制从光束开始到光束端点的直线。
if (scanBeginMapi != scanEndMapi){
updateLineBresenhami(scanBeginMapi, scanEndMapi);
}
}
//设置相关变量表示地图已经更新
this->setUpdated();
//增加更新索引（用于每次传入扫描仅更新网格单元一次）。
currUpdateIndex += 3;
}`
四、优缺点
1.优点
（1）不需要使用里程计，可以用于地面不平坦区域及空中飞行器。 （2）使用多分辨率地图能避免局部最小值。
2.缺点
（1）要求雷达更新频率较高，测量噪声小；或者机器人运动速度低。 （2）无法利用精确的里程计信息。
