最小二乘
正交
对于平面几何中的直线和向量来说,正交又称为垂直。 直线之间的垂直是指两条直线夹角为90°,其中一条直线在另一条直线上的投影为0。
** 最小二乘法的原理与要解决的问题**
最小二乘法是由勒让德在19世纪发现的,形式如下式:
$$ 标函数 = \sum(观测值-理论值)^2\\$$
观测值就是我们的多组样本,理论值就是我们的假设拟合函数。目标函数也就是在机器学习中常说的损失函数,我们的目标是得到使目标函数最小化时候的拟合函数的模型。举一个最简单的线性回归的简单例子,比如我们有
$m$ 个只有一个特征的样本:$(x_i, y_i)(i=1, 2, 3...,m)$
样本采用一般的$h_{\theta}(x)$ 为$n$ 次的多项式拟合,$h_{\theta}(x)=\theta_0+\theta_1x+\theta_2x^2+...\theta_nx^n,\theta(\theta_0,\theta_1,\theta_2,...,\theta_n)$ 为参数
最小二乘法就是要找到一组$\theta(\theta_0,\theta_1,\theta_2,...,\theta_n)$ 使得$\sum_{i=1}^n(h_{\theta}(x_i)-y_i)^2$ (残差平方和) 最小,即,求$min\sum_{i=1}^n(h_{\theta}(x_i)-y_i)^2$
勒让德在原文中提到:使误差平方和达到最小,在各方程的误差之间建立了一种平衡,从而防止了某一极端误差取得支配地位,而这有助于揭示系统的更接近真实的状态。至于说为什么最佳准则就是误差平方而不是其它的,当时是没有给出解释的,直到后来高斯建立了正态误差分析理论才成功回答了该问题。
误差分析理论其实说到底就一个结论:观察值的误差服从标准正态分布,即$ϵ ∈ N ( 0 , σ^2 ) $。
这个结论现在在我们看来是理所当然的,因为它实在太符合直觉了,观测值距离理论值有时大有时小,当观测样本多起来后,根据大数定理,这些样本的误差就一定会服从正态分布!
那么如何根据这个结论推导出最小二乘法呢?
我们先暂时忘记什么是最小二乘法,重新审视一下这个问题:我们观测得到了一组样本,我们想通过这组样本去估计出模型的参数。
我们假设真实的模型参数为 $ \theta $,模型的真实输出为$ f_{\theta}(x_i) $, 由于各种问题,我们观测到的样本$ y_{i}$距离真实值都是存在误差的,这个误差项记为ϵ \epsilonϵ。那么根据高斯误差分析的结论,误差项$ ϵ$应当满足$ ϵ ∈ N ( 0 , σ^2 )$ ,则每个观测样本$y_i $
应该有:$y_i ∈ N ( f_θ ( x_i ) , σ^2 ) $,即观察到的样本 $y_{i}$
是由理论值(模型的真实输出)$f_{\theta}(x_i)$叠加上高斯噪声 $ \epsilon$得到的,这个不难理解。
从概率统计的视角,我们把观测样本看作随机变量,其中随机变量$y_{i}$
符合概率分布:$y_{i} \in N\left(f_{\theta}(x_i), \sigma^{2}\right) $,目前已经给定了一批样本,那么我如何去估计出模型的参数呢?
没错,极大似然估计!
推导
极大似然估计的思想总结来说就是,最大化当前这个样本集发生的概率,专业点说就是最大化似然函数(likelihood function),而似然函数就是样本的联合概率。由于我们通常都会假设样本是相互独立的,因此联合概率就等于每个样本发生的概率乘积。
在这个问题中,每个样本 $y_{i}$
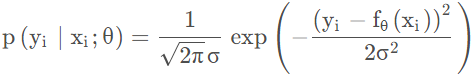
发生概率:
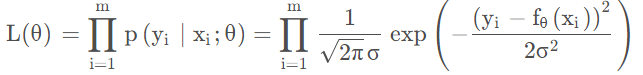
则似然函数:
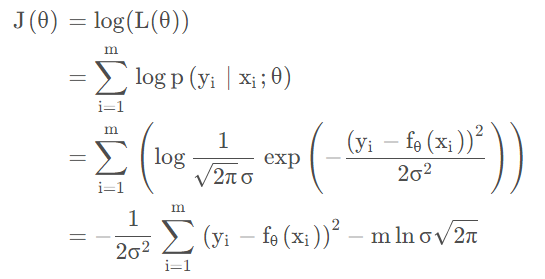
一般来说,我们会对似然函数取$log$以将连乘变成累加,主要有两个目的:防止溢出和方便求导,则有:
2π去掉不包含 $ \theta$ 的常数项,以及系数,则 $ \arg \max {\theta} J(\theta) \Leftrightarrow \arg \min {\theta} \sum{i=1}^{m}\left(y{i}-f_{\theta}(x_i)\right)^{2}$
即极大化似然函数等价于极小化最小二乘法的代价函数,这也表明了以误差平方和作为最佳拟合准则的合理性。
因此我们可以这样说,最小二乘法其实就是误差满足正态分布的极大似然估计!
最小二乘法的矩阵法解法
最小二乘法的代数法解法就是对
θi$\theta_i$ 求偏导数,令偏导数为0,再解方程组,得到
θi$\theta_i$ 。矩阵法比代数法要简洁,下面主要讲解下矩阵法解法,这里用多元线性回归例子来描:
假设函数$h_{\theta}(x_1,x_2,...x_n)=\theta_0+\theta_1x_1+...+\theta_nx_n$ 的矩阵表达方式为:
$$ h_{\theta}(\mathbf{x})=\mathbf{X}\theta\\$$
其中, 假设函数$h_{\theta}(\mathbf{x})=\mathbf{X}\theta$ 为$m\times1$ 的向量,$\theta$ 为$n\times1$ 的向量,里面有n 个代数法的模型参数。$X$ 为$m\times n$ 维的矩阵。$m$ 代表样本的个数,$n$ 代表样本的特征数。
损失函数定义为$J(\theta)=\frac{1}{2}(\mathbf{X}\theta-\mathbf{Y})^T(\mathbf{X}\theta-\mathbf{Y})$ ,其中$\mathbf{Y}$ 是样本的输出向量,维度为$m\times 1$ 。$\frac{1}{2}$ 在这主要是为了求导后系数为1,方便计算。根据最小二乘法的原理,我们要对这个损失函数对$\theta$ 向量求导取0。结果如下式:
$$ \frac{\partial }{\partial \theta}J(\theta)=\mathbf{X}^T(\mathbf{X}\theta-\mathbf{Y})=0\\$$
对上述求导等式整理后可得:
$$ \theta=(\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X}^T\mathbf{Y}\\$$
最小二乘法的几何解释
先说结论:最小二乘法的几何意义是高维空间中的一个向量在低维子空间的投影。
考虑这样一个简单的问题,求解二元一次方程组:
$$ \left\{\begin{matrix} x_1+x_2=3\leftarrow a\\ -x_1+x_2=1\leftarrow b \end{matrix}\right.\\$$
方程组的解也就是直线$a$与$b$的交点,并且很容易算出,$x_1=1,x_2=2$ .它的矩形形式:
$$ \begin{bmatrix}1\\ -1\end{bmatrix}\times x_1+\begin{bmatrix}1\\ 1\end{bmatrix}\times x_2=b\Leftrightarrow a_1\times x_1+a_2\times x_2=b\\$$
表示$x_1$ 倍的向量$a_1$ 加上$x_2$ 倍的向量$a_2$ 等于向量$b$ 。或者说,$b$ 是向量$a_1$ 与$a_2$ 的线性组合。

可以看到,1倍的$a_1$ 加上2倍的$a_2$ 既是$b$ ,而1和2正是我们的解。而最小二乘所面临的问题远不止两个点,拿三个点来说吧。(0,2),(1,2),(2,3)
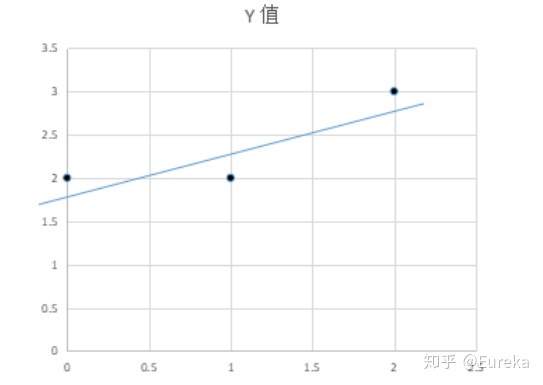
假设我们要找到一条直线$y=kx+b$ 穿过这三个点(虽然不可能),为表述方便,用$x_1$ 代替$k$ ,$x_2$ 代替$b$ :
$$ \left\{\begin{matrix}1\times k +b=2\\ 0\times k +b=2\\ 2\times k +b=3\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}1\times x_1 +x_2=2\\ 0\times x_1 +x_2=2\\ 2\times x_1 +x_2=3\end{matrix}\right.\Leftrightarrow \begin{bmatrix}1 &1 \\ 0 &1 \\ 2 &1 \end{bmatrix}\begin{bmatrix} x_1\\ x_2\end{bmatrix}=\begin{bmatrix}2\\ 2\\ 3\end{bmatrix}\Leftrightarrow A\times x=b\\$$
进一步的:
$$ \begin{bmatrix}1\\ 0\\ 2\end{bmatrix}\times x_1+\begin{bmatrix}1\\ 1\\ 1 \end{bmatrix}\times x_2=\begin{bmatrix}2\\2\\3\end{bmatrix}\Leftrightarrow a_1\times x_1 + a_2\times x_2=b\\$$
向量$b$ 是向量$a_1$ 与$a_2$ 的线性表示。用图形表示:
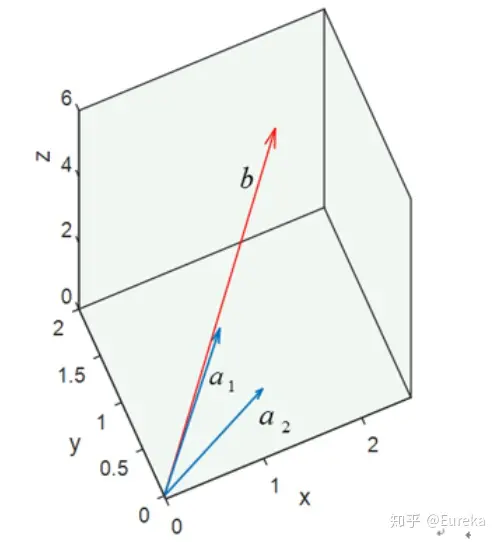
作图之后,我们惊讶的发现,无论我们怎样更改$a_1$ 和$a_2$ 的系数都不可能得到b,因为$a_1$ 与$a_2$ 的线性组合成的向量只能落在它们组成的子空间S里面,也就是说,向量$b$ 不在平面$S$ 上,虽然我们找不到这样的向量,但在$S$ 上找一个比较接近的可以吧。很自然的想法就是将向量$b$ 投影在平面$S$ 上,投影在$S$ 上的向量$P$ 就是$b$ 的近似向量,并且方程$A\hat{x}=P$ $是有解的。
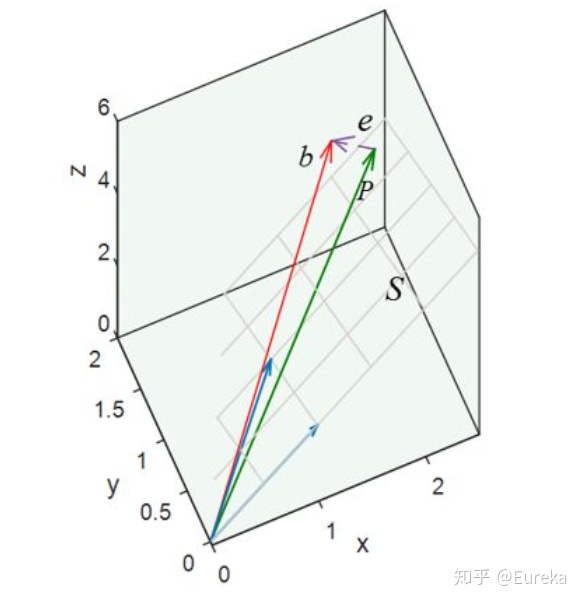
这个误差最小的时候就是$e$ 正交与平面$S$ ,也正交与$S$ 中的向量,$a_1,a_2$ (矩阵$A$ 的列向量),即点乘为0,$a_1^Te=0$ ,$a_2^Te=0$ 矩阵表示:
$$ A^Te=0\\$$
$$ A^T(b-A\hat{x})=0\\ $$ $$ A^TA\hat{x}=A^Tb\\ $$所以,我们可以得出,它的几何意义就是高维空间中的一个向量在低维子空间上的投影。
最小二乘法的局限性和适用场景
从上面可以看出,最小二乘法适用简洁高效,比梯度下降这样的迭代法似乎方便很多。但是这里我们就聊聊最小二乘法的局限性。
首先,最小二乘法需要计算$X^TX$ 的逆矩阵,有可能它的逆矩阵不存在,这样就没有办法直接用最小二乘法了,此时梯度下降法仍然可以使用。当然,我们可以通过对样本数据进行整理,去掉冗余特征。让$X^TX$ 的行列式不为0,然后继续使用最小二乘法。
第二,当样本特征$n$ 非常的大的时候,计算$X^TX$ 的逆矩阵是一个非常耗时的工作($n\times n$ 的矩阵求逆),甚至不可行。此时以梯度下降为代表的迭代法仍然可以使用。那这个$n$ 到底多大就不适合最小二乘法呢?如果你没有很多的分布式大数据计算资源,建议超过10000个特征就用迭代法吧。或者通过主成分分析降低特征的维度后再用最小二乘法。
第三,如果拟合函数不是线性的,这时无法使用最小二乘法,需要通过一些技巧转化为线性才能使用,此时梯度下降仍然可以用。
参考
最小二乘法(least sqaure method) - 知乎 (zhihu.com)
