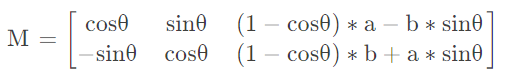仿射变换

仿射变换也称仿射投影，是指几何中，对一个向量空间进行线性变换并接上一个平移，变换为另一个向量空间。所以，仿射变换其实也就是再讲如何来进行两个向量空间的变换

假设有一个向量空间k

k=(x,y)

还有一个向量空间j

j=(x′,y′)

想要将向量空间由k变为j ，可以通过下面的公式进行变换

j=k∗w+b

上式进行拆分可得

将上式转换为矩阵的乘法

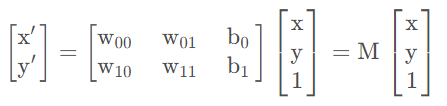
通过参数矩阵w就可以实现两个向量空间之间的转换，在进行仿射变换的时候我们也只需要一个矩阵w就可以实现平移、缩放、旋转和翻转变换。

平移

在平面坐标系有点P(x,y)和点P'(x',y')，如果我们想要将P点移动到P'通过下面的变换就可以实现

x′=x+Δx
y′=y+Δy

Δx和Δy就是x方向上和y方向上的偏移量，我们将其转换为矩阵的形式

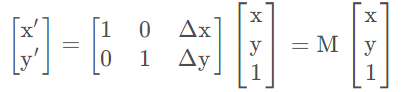
翻转

有时候我们我们需要对图像进行水平翻转、垂直翻转、镜像翻转(同时进行水平和垂直翻转)，想要实现这个功能并不难

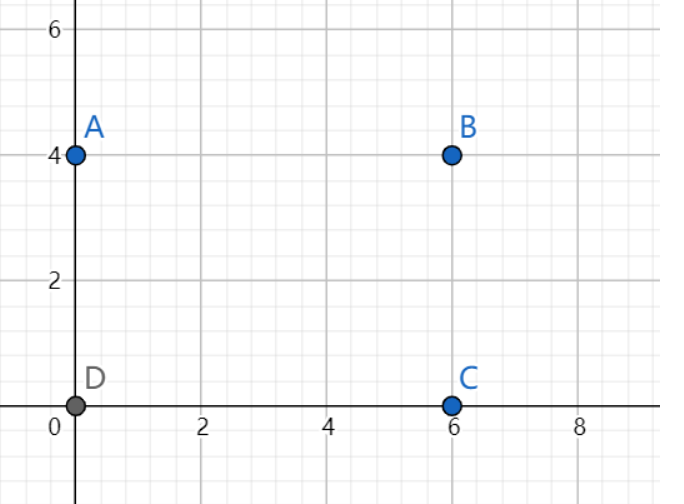
上图中的 A、B、C、D表示图像的四个顶点，如果我们需要对图像进行水平翻转，那么我们就需要将A点和B点进行交换，C点和D点进行交换，沿着x轴的中线进行对称交换位置，通过下面的式子可以实现水平翻转

x′ = −x+w

上式中的w表示图像的宽，同理可得垂直翻转的实现公式

y′ = −y+h

上式中的h表示的是图像的高

缩放

如果我们想要对坐标系的P PP点进行缩放操作，通过下面的公式就可以实现

x′ = fx ∗ x 
y ′= fy ∗ y 

通过，在x和y前面添加一个缩放系数即可，同样我们将其转换为矩阵形式

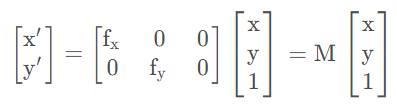
旋转

围绕原点旋转

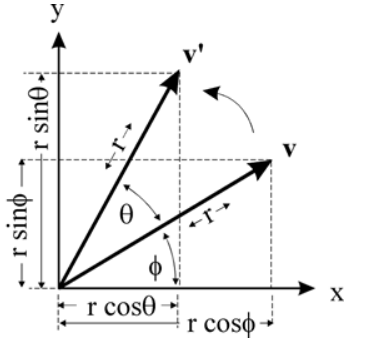
上图中点v在围绕原点旋转θ 度之后得到了点v′,我们将坐标点用极坐标的形式来表示可以得到v(rcosϕ,rsinϕ)，所以v′(r cos(θ+ϕ) , r sin(θ+ϕ)) 利用正弦和余弦将其展开可得

对于v点来说：
    x=rcosϕ
    y=rsinϕ
对于v′来说：
    x′=rcos(θ+ϕ)
      =rcosθ∗cosϕ−rsinθ∗sinϕ
    y′=rsin(θ+ϕ)
      =rsinθ∗cosϕ+rcosθ∗sinϕ
然后再将x和y代入上式，可得
    x′=x∗cosθ−y∗sinθ
    y′=x∗sinθ+y∗cosθ

再将上式用矩阵M MM表示，可得

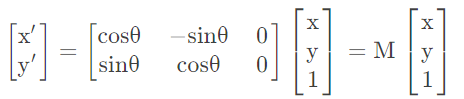
特别注意：我们在建立直角坐标系的时候是以左下角为原点建立的，然而对于图像而言是以左上角为原点建立的，所以我们需要对角度θ进行取反，结合三角函数的特性，M矩阵的表达式如下

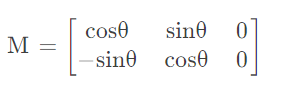
围绕任意点旋转

如果我们想围绕任意坐标点旋转呢？其实也并不难，下图的v点在围绕c点(a,b)旋转90度得到v'。其实我们可以将其等价于，先将v vv点平移到v1点，然后再将v1点围绕原点旋转90度得到v2点,最后再将v2点沿着v vv点平移的反方向平移相同长度，最终得到v'。这样我们就将围绕任意坐标点旋转的问题转换成了围绕原点旋转的问题

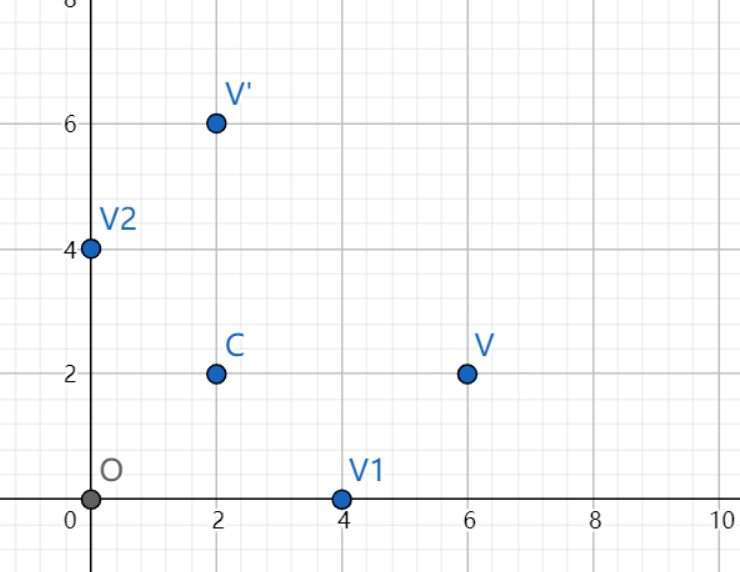
在围绕原点旋转变换公式的基础上，我们将其改进为围绕任意点c(a,b)旋转，我们现在原来的坐标进行平移，得到变换后的坐标，最后再沿着之前平移的反方向进行平移，就得到围绕任意点旋转的变换公式：

x′=(x−a)∗cosθ−(y−b)∗sinθ+a
y′=(x−a)∗sinθ+(y−b)∗cosθ+b

其展开可得

x′=x∗cosθ−y∗sinθ+(1−cosθ)∗a+b∗sinθ
y′=x∗sinθ+y∗cosθ+(1−cosθ)∗b−a∗sinθ 

上式中的c(a,b)表示旋转中心，因为坐标系问题需要对θ \thetaθ进行取反，最终M MM矩阵的表达式如下